
【题目】如图:在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() 是最大的负整数,且
是最大的负整数,且![]() 满足
满足![]() .
.
![]()
(1)a=________,b=________,c=________.
(2)若将数轴折叠,使得点![]() 与点
与点![]() 重合,则点
重合,则点![]() 与数________表示的点重合;
与数________表示的点重合;
(3)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒2个单位长度和3个单位长度的速度向右运动,假设
分别以每秒2个单位长度和3个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,则
,则![]() ________,
________,![]() ________.(用含
________.(用含![]() 的代数式表示)
的代数式表示)
(4)![]() 的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
【答案】(1)-3;-1;5;(2)3;(3)![]() ,
,![]() ;(4)
;(4)![]() 的值为定值16.
的值为定值16.
【解析】
(1)根据b为最大的负整数可得出b的值,再根据绝对值以及偶次方的非负性即可得出a、c的值;
(2)根据折叠的性质结合a、b、c的值,即可找出与点B重合的数;
(3)根据运动的方向和速度结合a、b、c的值,即可找出t秒后点A、B、C分别表示的数,利用两点间的距离即可求出AB、BC的值;
(4)将(3)的结论代入3BC-AB中,可得出3BC-AB为定值16,此题得解.
(1)∵![]() 是最大的负整数,且
是最大的负整数,且![]() 满足
满足![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
故答案为:-3;-1;5.
(2)![]() .
.
故答案为:3.
(3)t秒钟过后,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点C表示的数为
,点C表示的数为![]() ,
,
∴![]() ,
,![]() .
.
故答案为:![]() ,
,![]() .
.
(4)∵![]() ,
,![]() ,
,
∴![]()
![]() .
.
∴![]() 的值为定值16.
的值为定值16.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】为了提倡节约用电,某地区规定每月用电量不超过 a 千瓦·时,居民生活用电基本价格为每千瓦时 0.5 元;若每月用电量超过 a 千瓦·时,则超过部分按基本电价提高 20%收费.居住此地的老李家二月份用电 120 千瓦·时,所交的电费为 66 元.
(1)求 a 的值;
(2)老李登录当地国家电网网络平台缴费后弹出一个对话框:您的家庭一月份和二月份的平均电费不超过0.54 元/千瓦·时,评为“节能小家庭”.试计算老李家一月份的用电量的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
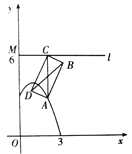
【题目】如图,点A在抛物线![]() 上,直线
上,直线![]() ⊥y轴于点M,AC⊥
⊥y轴于点M,AC⊥![]() 于点C,以AC为对角线作矩形ABCD,若点M的坐标为(0,6),则BD的取值范围是_______.
于点C,以AC为对角线作矩形ABCD,若点M的坐标为(0,6),则BD的取值范围是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列函数图象上任取不同两点P(x1,y1),Q(x2,y2),一定能使(x2﹣x1)(y2﹣y1)>0成立的是( )
A.y=﹣2x+1(x<0)B.y=﹣x2﹣2x+8(x<0)
C.y=![]() (x>0)D.y=2x2+x﹣6(x>0)
(x>0)D.y=2x2+x﹣6(x>0)
查看答案和解析>>
科目:初中数学 来源: 题型:
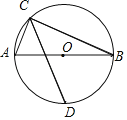
【题目】如图,AB是⊙O的直径,点C是⊙O上一点(点C不与A,B重合),连接CA,CB.∠ACB的平分线CD与⊙O交于点D.
(1)求∠ACD的度数;
(2)探究CA,CB,CD三者之间的等量关系,并证明;
(3)E为⊙O外一点,满足ED=BD,AB=5,AE=3,若点P为AE中点,求PO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
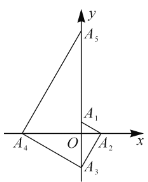
【题目】如图,已致点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ;过点
;过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ;过点
;过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ;……;按此规律进行下去,则点
;……;按此规律进行下去,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
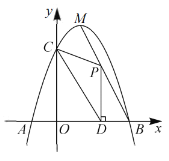
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() ,
,![]() 是抛物线的顶点,直线
是抛物线的顶点,直线![]() 是抛物线的对称轴,且点
是抛物线的对称轴,且点![]() 的坐标为
的坐标为![]() .
.
(1)求抛物线的解析式.
(2)已知![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() .若
.若![]() 的面积为
的面积为![]() .
.
①求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 取得最值时,求点
取得最值时,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?如果存在,请求出点
为等腰三角形?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆![]() 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.

小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置… | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | … |
BC | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | … |
OD | 6.71 | 7.24 | 7.07 | 6.71 | 6.16 | 5.33 | … |
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三位数t=![]() (其中a、b、c不全相等且都不为0),重新排列各数位上的数字必可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为T(t).例如,539的差数T(539)=953﹣359=594.
(其中a、b、c不全相等且都不为0),重新排列各数位上的数字必可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为T(t).例如,539的差数T(539)=953﹣359=594.
(1)根据以上方法求出T(268)= ,T(513)= ;
(2)已知三位数![]() (其中a>b>1)的差数T(
(其中a>b>1)的差数T(![]() )=495,且各数位上的数字之和为3的倍数,求所有符合条件的三位数的值.
)=495,且各数位上的数字之和为3的倍数,求所有符合条件的三位数的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com