
【题目】四边形 ABCD 中,E 为边 BC 上一点,F 为边 CD 上一点,且∠AEF=90°.
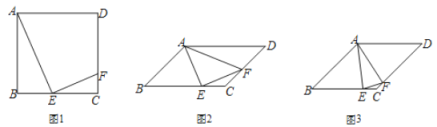
(1)如图 1,若 ABCD 为正方形,E 为 BC 中点,求证:![]() .
.
(2)若 ABCD 为平行四边形,∠AFE=∠ADC,
①如图 2,若∠AFE=60°,求![]() 的值;
的值;
②如图 3,若 AB=BC,EC=2CF.直接写出 cos∠AFE 值为 .
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】
(1)如图1中,设正方形的边长为2a.只要证明△ABE∽△ECF,可得![]() ,求出CF、DF即可解决问题;
,求出CF、DF即可解决问题;
(2)如图2中,在AD上取一点H,使得FH=DF.只要证明△AEF是等边三角形,推出AF=2EF,再证明△AHF∽△FCE,可得EC:HF=EF:AF=1:2;
(3)如图3,作FT=FD交AD于点T,作FH⊥AD于H,证△FCE∽△ATF,设CF=2,则CE=4,可设AT=x,则TF=2x,AD=CD=2x+2,DH=![]() DT=
DT=![]() ,分别用含x的代数式表示出∠AFE和∠D的余弦值,列出方程,求出x的值,即可求出结论.
,分别用含x的代数式表示出∠AFE和∠D的余弦值,列出方程,求出x的值,即可求出结论.
(1)证明:如图1中,设正方形的边长为2a.
∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∵∠AEF=90°,
∴∠AEB+∠FEC=90°,∠FEC+∠EFC=90°,
∴∠AEB=∠EFC,
∴△ABE∽△ECF,
∴![]()
∵BE=EC=a,AB=CD=2a,
∴CF=![]() a,DF=CDCF=
a,DF=CDCF=![]() a,
a,
∴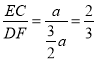 ;
;
(2)如图2中,在AD上取一点H,使得FH=DF,
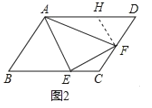
∵∠AEF=90°,∠AFE=∠D=60°,
∴AF=2EF,
∵FH=DF,
∴△DHF是等边三角形,
∴∠FHD=60°,
∴∠AHF=120°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C=180°∠D=120°,
∴∠AHF=∠C,
∵∠AFC=∠D+∠FAH=∠EFC+∠AFE,∠AFE=∠D,
∴∠HAF=∠EFC,
∴△AHF∽△FCE,
∴EC:HF=EF:AF=1:2,
∴![]() ;
;
如图3,作FT=FD交AD于点T,作FH⊥AD于H,
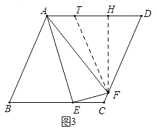
则∠FTD=∠FDT,
∴180°∠FTD=180°∠D,
∴∠ATF=∠C,
又∵∠TAF+∠D=∠AFE+∠CFE,且∠D=∠AFE,
∴∠TAF=∠CFE,
∴△FCE∽△ATF,
∴![]() =
=![]() ,
,
设CF=2,则CE=4,可设AT=x,则TF=2x,AD=CD=2x+2,
∴DH=![]() DT=
DT=![]() ,且
,且![]() ,
,
由cos∠AFE=cos∠D,得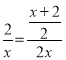 ,
,
解得x=6,(x=0舍去)
∴cos∠AFE=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(抗击疫情)为了遏制新型冠状病毒疫情的蔓延势头,各地教育部门在推迟各级学校开学时间的同时提出“听课不停学”的要求,各地学校也都开展了远程网络教学,某校集中为学生提供四类在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据结果绘制成如下两幅不完整的统计图。
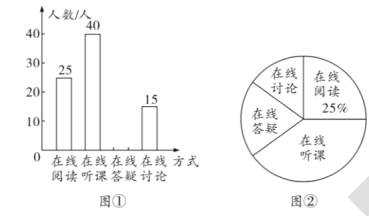
(1)本次调查的人数有多少人?
(2)请补全条形图;
(3)请求出“在线答疑”在扇形图中的圆心角度数;
(4)小宁和小娟都参加了远程网络教学活动,请求出小宁和小娟选择同一种学习方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
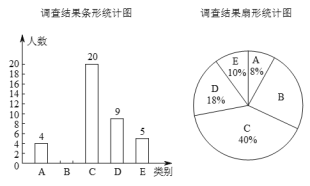
【题目】当今社会手机越来越普遍,有很多人每天过分依赖手机,每天使用手机时间过长而形成了“手机瘾”.为了解某高校大学生每天使用手机时间的情况,某社团随机调查了部分学生使用手机的时间,将调查结果分为五类:A.基本不用;B.平均每天使用1~2小时;C.平均每天使用2~4小时;D.平均每天使用4~6小时;E.平均每天使用超过6小时并把所得数据绘制成如图两幅不完整的统计图,请根据相关信息,解答下列问题:
(1)将条形统计图补充完整;
(2)若每天使用手机的时间超过6小时,则患有严重的“手机瘾”.该校共有学生14900人,试估计该校约有多少人患有严重的“手机瘾”;
(3)在被调查的基本不使用手机的4位同学中有2男2女,现要从中随机抽取两名同学去参加座谈会,请你用列表法或树状图法求出所选两位同学恰好是一名男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
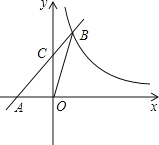
【题目】如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y=![]() 在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<
在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<![]() 的解集是0<x<1.其中正确的有( )
的解集是0<x<1.其中正确的有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
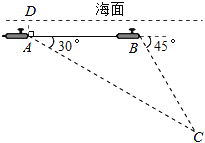
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com