
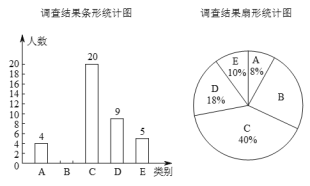
����Ŀ����������ֻ�Խ��Խ�ձ飬�кܶ���ÿ����������ֻ���ÿ��ʹ���ֻ�ʱ��������γ��ˡ��ֻ���Ϊ�˽�ij��У��ѧ��ÿ��ʹ���ֻ�ʱ��������ij������������˲���ѧ��ʹ���ֻ���ʱ�䣬����������Ϊ���ࣺA���������ã�B��ƽ��ÿ��ʹ��1��2Сʱ��C��ƽ��ÿ��ʹ��2��4Сʱ��D��ƽ��ÿ��ʹ��4��6Сʱ��E��ƽ��ÿ��ʹ�ó���6Сʱ�����������ݻ��Ƴ���ͼ������������ͳ��ͼ������������Ϣ������������⣺
��1��������ͳ��ͼ����������
��2����ÿ��ʹ���ֻ���ʱ�䳬��6Сʱ���������ص����ֻ��������У����ѧ��14900�ˣ��Թ��Ƹ�УԼ�ж����˻������صġ��ֻ���
��3���ڱ�����Ļ�����ʹ���ֻ���4λͬѧ����2��2Ů����Ҫ���������ȡ����ͬѧȥ�μ���̸�ᣬ�������б�������״ͼ�������ѡ��λͬѧǡ����һ����ͬѧ��һλŮͬѧ�ĸ��ʣ�
���𰸡���1����������2��1490����3����������![]()
��������
��1��������ã������ѧ����Ϊ��4��8%=50�������B�����������ɲ�ȫͳ��ͼ��
��2��������ɵã���Уѧ���������صġ��ֻ���Լ�У�1490��10%=149��������
��3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ������λͬѧǡ����һ����ͬѧ��һλŮͬѧ������������ø��ʹ�ʽ������ô𰸣�
��:��1����������ͳ��ͼ��;

�����ѧ��������Ϊ:
![]() ���ˣ�
���ˣ�
B���ѧ������Ϊ:
![]() ���ˣ�.
���ˣ�.
��2��![]() ���ˣ�
���ˣ�
��:��УԼ��1490�˻������ص����ֻ����;
��3������״ͼ����:
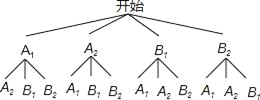
����״ͼ��֪,����12�ֵȿ��ܵĽ��,����ǡ����һ����ͬѧ��һ��Ůͬѧ�������8��,������ѡ��λͬѧǡ����һ��һŮ�ĸ���Ϊ![]() .
.


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
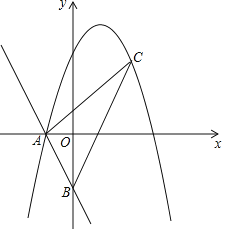
����Ŀ��һ�κ���y����2x��2�ֱ���x�ᡢy�ύ�ڵ�A��B������Ϊ��1��4���������߾�����A��
��1���������ߵĽ���ʽ��
��2����CΪ��һ������������һ���㣮���C�ĺ�����Ϊm����ABC�����ΪS����mΪ��ֵʱ��S��ֵ�����S�����ֵ��
��3���ڣ�2���Ľ����£�����M��y���ϣ���ACMΪֱ�������Σ���ֱ��д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����¹ڷ��ס���Ű����������Ӣ��ӿ�֣�������λ����Ӣ��������ɽ�������ꡢ���������Ŷ�����μ�ΪA��B��C��D����Ϊ��ͬѧ���˽���λ���¼�����ʦ������»��ȡ������ȫ��ͬ�Ŀ�Ƭ���ֱ�д��A��B��C��D�ĸ���ţ�Ȼ���泯�Ϸ��ã����Ⱥ�ÿ��ͬѧ���������ȡһ�ţ����±�ź�Żأ���ʦҪ��ÿλͬѧ���ݳ鵽�Ŀ�Ƭ�ϵı�Ų�����Ӧ����Ӣ�۵����ϣ�������С����

��1��������ֿ�Ƭ������鵽���ΪC�ĸ���Ϊ�� ����
��2��ƽƽ�Ͱ�����λͬѧ�鵽�Ŀ�Ƭ�Dz�ͬӢ�۵ĸ����Ƕ��٣�����״ͼ���б��ķ�����ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı��� ABCD �У�E Ϊ�� BC ��һ�㣬F Ϊ�� CD ��һ�㣬�ҡ�AEF=90����
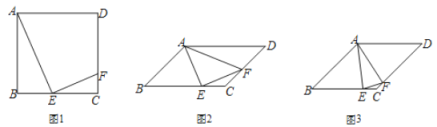
��1����ͼ 1���� ABCD Ϊ�����Σ�E Ϊ BC �е㣬��֤��![]() ��
��
��2���� ABCD Ϊƽ���ı��Σ���AFE=��ADC��
����ͼ 2������AFE=60������![]() ��ֵ��
��ֵ��
����ͼ 3���� AB=BC��EC=2CF��ֱ��д�� cos��AFE ֵΪ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
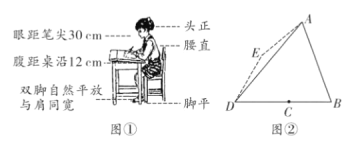
����Ŀ�����õ�����ϰ��������������������������������彡������ô����Ҫ����ȷ��д�����ˣ������ϰ벿��ֱ��ͷ��������Ŀ��ǰ�������ַ��������ϣ�����ƽ�ţ�����ͦ������״̬�£���ͼ�٣���ͼ���е��۾���Ϊ��![]() ��������Ϊ��
��������Ϊ��![]() ���ʼ��Ϊ��
���ʼ��Ϊ��![]() ����
����![]() �������صĽ����Ϊ��
�������صĽ����Ϊ��![]() ����֪
����֪![]() ����
����![]() ��
��![]() �ľ���Ϊ23cm��
�ľ���Ϊ23cm�� ![]() ��
��
��1����![]() �Ķ���
�Ķ���
��2����ʦ����С��ͬѧд�����Ʋ���ȷ���۾���б��ͼ2�ĵ�![]() ����
����![]() ǡ����
ǡ����![]() �Ĵ�ֱƽ�����ϣ���
�Ĵ�ֱƽ�����ϣ���![]() ������Ҫ�������Ϊ��ȷ�����ƣ����۾����ڵ�λ�������ľ��루�����ȷ��1cm��
������Ҫ�������Ϊ��ȷ�����ƣ����۾����ڵ�λ�������ľ��루�����ȷ��1cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��y��x+4��������y����![]() x2+bx+c��b��c�dz���������A��B���㣬��A��x���ϣ���B��y���ϣ�����������x�����һ������Ϊ��C��
x2+bx+c��b��c�dz���������A��B���㣬��A��x���ϣ���B��y���ϣ�����������x�����һ������Ϊ��C��

��1����������ߵĽ���ʽ��
��2��P����������һ���㣨�����A��B�غϣ���
����ͼ2������P��ֱ��AB�Ϸ�������OP��AB�ڵ�D����![]() �����ֵ��
�����ֵ��
����ͼ3������P��x����Ϸ�������PC����PCΪ����������CPEF�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣮������E��Fǡ������y���ϣ�ֱ��д����Ӧ�ĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC�У���ACB��90����EΪAB��һ�㣬��AEΪֱ������O��BC�����ڵ�D������ED���ӳ���AC���ӳ����ڵ�F��
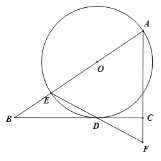
��1����֤��AE��AF��
��2����BC��4��AC��3������O�İ뾶����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
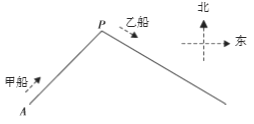
����Ŀ��С��![]() �ڸۿ�
�ڸۿ�![]() ����ƫ��45��������ۿ�81���ﴦ���״���
����ƫ��45��������ۿ�81���ﴦ���״���![]() ��������
��������![]() ������6����/ʱ���ٶ�ʻ��ۿڣ��Ҵ��Ӹۿ�
������6����/ʱ���ٶ�ʻ��ۿڣ��Ҵ��Ӹۿ�![]() ����������ƫ��60��������15����/ʱ���ٶ�ʻ��ۿڣ�������ͬʱ������
����������ƫ��60��������15����/ʱ���ٶ�ʻ��ۿڣ�������ͬʱ������
��1�������� Сʱ������ۿ�![]() �ľ�����ȣ�
�ľ�����ȣ�
��2��������Сʱ���Ҵ��ڼ״�����������?(�����ȷ��0.1Сʱ���ο����ݣ�![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
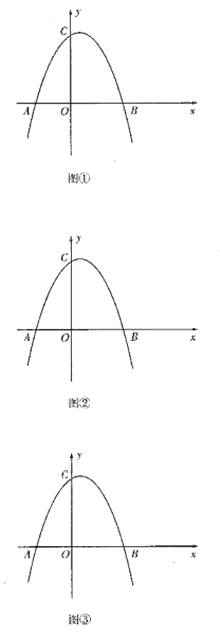
����Ŀ����ͼ�������߽�![]() ����
����![]() ��
��![]() ����
����![]() ����
����![]() ��
��
��1���������߽���ʽ��
��2����![]() �ڵ�һ�����������ϣ�
�ڵ�һ�����������ϣ�![]() ��
��![]() �������Ϊ
�������Ϊ![]() �����
�����![]() �����ꣻ
�����ꣻ
��3���ڣ�2���������£��ڵ�![]() ��
��![]() ֮�����������ȡ��
֮�����������ȡ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() �ӳ�����
�ӳ�����![]() ����
����![]() ʱ�����
ʱ�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com