
����Ŀ��ij��ҵΪ��Ӧ���ҽ�����ƶ�ĺ��٣�������ij����ȫ��ƶ����������ѧ����������������ѧ��ÿ������200Ԫ������ѧ��ÿ������300Ԫ����֪�����������ij���ѧ���������������ĸ���ѧ��������2�����Ҹ���ҵ��2018���°���7��12����6��������ѧ����֧��10.5��Ԫ��
��1���ʸ�����ֱ��ж���������ѧ������ѧ�������������
��2��2018��7��12���ڼ䣬�������ij�������ѧ���У��ֱ���30%��40%��ѧ������Ϊ����ѧ�����Ӷ�����˸����������Ĺ������ͬʱ���ṩ��������ҵΪ�˼�������������ѧ���Ľ�ȡ�ĺ�ѧϰ���飬������2019���ϰ���1��6�±���Ϊ����ѧ���ij���ѧ��ÿ��ÿ������a%���������Ա���Ϊ����ѧ���ĸ���ѧ��ÿ��ÿ������2a%���������ڴ˽������ߵĹ����£�2019��1��6�±���Ϊ����ѧ���ij�������ѧ���քe��2018��7��12�µ�����������3a%��a%��������2019���ϰ�����Ϊ����ѧ���ij�������ѧ������õ������ܽ��һ���¾ʹﵽ��10800Ԫ����a��ֵ��
���𰸡���1��50��25����2��20
��������
��1���Ƚ�10.5��Ԫ��Ϊ105000Ԫ�����������![]() ������ѧ����������������������2x������ѧ���ܵ��������������һԪһ�η��̣���⼴�ɣ�
������ѧ����������������������2x������ѧ���ܵ��������������һԪһ�η��̣���⼴�ɣ�
��2������2019���ϰ�����Ϊ����ѧ���ij�������ѧ������õ������ܽ��һ���¾ʹﵽ��10800Ԫ��Ϊ������ϵ���г����̣�Ȼ����a%��t����Ϊ����t��һԪ���η��̣�����t���ٸ���a%��t�����a���ɣ�
��1��10.5��Ԫ��105000Ԫ
���������![]() ������ѧ����������������������
������ѧ����������������������![]() ������ѧ���ܵ�������������ã�
������ѧ���ܵ�������������ã�
![]()
��ã�![]()
��![]()
�������ֱ���50������ѧ����25������ѧ�������������
��2��������ã�
![]()
��![]()
��![]() ���̻�Ϊ��
���̻�Ϊ��![]()
��![]()
���![]() ���ᣩ��
���ᣩ��![]()
��![]() ��
��


 ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д� 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�A![]() ��B
��B![]() ��C
��C![]() ����PΪ����һ�㣬��֪PA��PB�����߶�PC�����ֵΪ�� ��
����PΪ����һ�㣬��֪PA��PB�����߶�PC�����ֵΪ�� ��
A.3B.5C.8D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() �����ߣ�����
�����ߣ�����![]() ��
��![]() ��E������A��
��E������A��![]() ��F����
��F����![]() ��D������
��D������![]() ��
��![]() ��
��
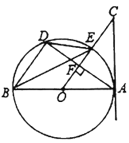
��1����֤��![]() ��
��
��2����![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF=��GAC��
��1����֤����ADE�ס�ABC��
��2����AD=3��AB=5����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���д��������A��B��C����ˮ�����üס��ҡ������ַ�ʽ����װ����н������ۣ�ÿ�е��ܳɱ�Ϊ����A��B��C����ˮ���ɱ�֮�ͣ����ӳɱ����Բ��ƣ����ַ�ʽÿ�зֱ�װA��B��C����ˮ��6kg��3kg��1kg�����ַ�ʽÿ�зֱ�װA��B��C����ˮ��2kg��6kg��2kg����ÿ�е��ܳɱ���ÿǧ��Aˮ���ɱ���12.5����ÿ�м�����������Ϊ20%��ÿ�мױ�ÿ���ҵ��ۼ۵�25%��ÿ�б��ڳɱ������40%��ۺ����۳��ۣ�����Ϊÿǧ��Aˮ���ɱ���1.2���������ۼס��ҡ������ַ�ʽ������������֮��Ϊ2��2��5ʱ����������������Ϊ_____���������ʣ��������ɱ���100%��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� C Ϊ Rt��ACB �� Rt��DCE �Ĺ���������ACB=��DCE=90������ �� AD��BE������ C �� CF��AD �ڵ� F���ӳ� FC �� BE �ڵ� G���� AC=BC=25��CE=15�� DC=20����![]() ��ֵΪ___________��
��ֵΪ___________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
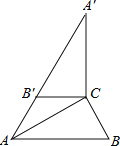
����Ŀ����ͼ������ABC�У���ACB��90������B��60����BC��2������ABC�Ƶ�C˳ʱ����ת���õ���A��B��C������AB������A��B����A����ͬһ��ֱ���ϣ���AA����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ����(1��0)�͵�(0����3)���Ҷ����ڵ������ޣ���m��a��b��c����m��ȡֵ��Χ�ǣ� ��
����(1��0)�͵�(0����3)���Ҷ����ڵ������ޣ���m��a��b��c����m��ȡֵ��Χ�ǣ� ��
A.��6��m��0B.��6��m����3C.��3��m��0D.��3��m����1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90����DΪAB���е㣬��CDΪֱ���ġ�O��BC�ڵ�E������E��EF��AB�ڵ�F��
��1���ж�EF����ֱ�����O��λ�ù�ϵ����˵�����ɣ�
��2������B��40������O�İ뾶Ϊ6����![]() �ij����������������
�ij����������������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com