
【题目】在平面直角坐标系中,A![]() ,B
,B![]() ,C
,C![]() ,点P为任意一点,已知PA⊥PB,则线段PC的最大值为( )
,点P为任意一点,已知PA⊥PB,则线段PC的最大值为( )
A.3B.5C.8D.10
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]() 的顶点为A,抛物线
的顶点为A,抛物线![]() 的顶点为B,其中m≠﹣2,抛物线
的顶点为B,其中m≠﹣2,抛物线![]() 与
与![]() 相交于点P.
相交于点P.
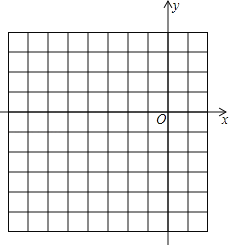
(1)当m=﹣3时,在所给的平面直角坐标系中画出C1,C2的图象;
(2)已知点C(﹣2,1),求证:点A,B,C三点共线;
(3)设点P的纵坐标为q,求q的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1.有下列结论:①b2=4ac ②abc>0 ③a>c ④4a+c>2b.其中结论正确的个数是( )
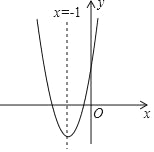
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:抛物线y=x2+bx+c与直线y=﹣x﹣1交于点A,B.其中点B的横坐标为2.点P(m,n)是线段AB上的动点.
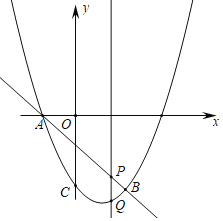
(1)求抛物线的表达式;
(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平角直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形,在(2)的情况下,在平面内找出所有符合要求的整点R,使P、Q、B、R为整点平行四边形,请直接写出整点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东55方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
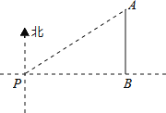
A.2cos55o海里B.![]() 海里C.2sin55海里D.
海里C.2sin55海里D.![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学利用寒假30天时间贩卖草莓,了解到某品种草莓成本为10元/千克,在第![]() 天的销售量与销售单价如下(每天内单价和销售量保持一致):
天的销售量与销售单价如下(每天内单价和销售量保持一致):
销售量 |
|
销售单价 | 当 |
当 |
设第![]() 天的利润
天的利润![]() 元.
元.
(1)请计算第几天该品种草莓的销售单价为25元/千克?
(2)这30天中,该同学第几天获得的利润最大?最大利润是多少?注:利润=(售价-成本)×销售量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与x轴相交于点A反比例函数
的图象与x轴相交于点A反比例函数![]() 相交于
相交于![]() 两点.
两点.

(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)连接OB,OC,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业为响应国家教育扶贫的号召,决定对某乡镇全体贫困初、高中学生进行资助,初中学生每月资助200元,高中学生每月资助300元.已知该乡受资助的初中学生人数是受资助的高中学生人数的2倍,且该企业在2018年下半年7﹣12月这6个月资助学生共支出10.5万元.
(1)问该乡镇分别有多少名初中学生和高中学生获得了资助?
(2)2018年7﹣12月期间,受资助的初、高中学生中,分别有30%和40%的学生被评为优秀学生,从而获得了该乡镇政府的公开表扬.同时,提供资助的企业为了激发更多受资助学生的进取心和学习热情,决定对2019年上半年1﹣6月被评为优秀学生的初中学生每人每月增加a%的资助,对被评为优秀学生的高中学生每人每月增加2a%的资助.在此奖励政策的鼓励下,2019年1﹣6月被评为优秀学生的初、高中学生分別比2018年7﹣12月的人数增加了3a%、a%.这样,2019年上半年评为优秀学生的初、高中学生所获得的资助总金额一个月就达到了10800元,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com