【题目】如图，
是⊙
的直径，弦
,垂足为
，
，连结
，
为的中点，连结
，过点
作直线
，交的延长线于点
．
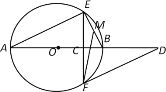
（1）求证：
是⊙的切线；
（2）若
，求⊙的半径
【答案】（1）见解析；（2）2
【解析】
（1）连接OE，OF，利用垂径定理及等腰三角形的性质得到∠DOF=∠DOE．而∠DOE=2∠A，所以
，由 
得到
，
于是可求出
，所以
为⊙
的切线；
（2）连接OM，如图，利用圆周角定理得到∠AEB=90°．再证明OM∥AE得到∠MOB=∠A=30°．而∠DOF=2∠A=60°，所以∠MOF=90°，设⊙O的半径为r，利用含30度的直角三角形三边的关系得OM，然后根据勾股定理列出方程求解即可．
解：（1）如图，连结
，
，
∵
，
是⊙的直径
∴
，
∵
，
，
∴
∵，
∴，
∴
∴为⊙的切线
（2）连接
，
∵
为⊙的直径，
∴为中点，
，
∵
为
的中点，
∴
，
设⊙的半径为
．
∵，
∴
，
∴
．
∵
,，
∴
∵
∴
∴
，
∵
，
∴
.
解得
．（舍去负根）
∴⊙的半径为2.
科目：初中数学 来源： 题型：
【题目】为进一步提高全民“节约用水”意识，某学校组织学生进行家庭月用水量情况调查活动，李明随机抽查了所住小区x户家庭的月用水量，绘制了下面不完整的统计图：
（1）求x并补全条形统计图；
（2）求这x户家庭的月平均用水量；并估计李明所住小区620户家庭中月用水量低于月平均用水量的家庭户数；
（3）从月用水量为5m3和9m3的家庭中任选两户进行用水情况问卷调查，求选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率；
查看答案和解析>>
科目：初中数学 来源： 题型：
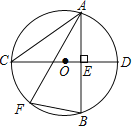
【题目】如图，已知⊙O的半径是5，AB是⊙O的弦，直径CD⊥AB于点E．
（1）点F是⊙O上任意一点，请仅用无刻度的直尺画出∠AFB的角平分线；
（2）若AC＝8，试求AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于一个函数，当自变量x取n时，函数值y等于4－n，我们称n为这个函数的“二合点”，如果二次函数y＝mx2+x+1有两个相异的二合点x1，x2，且x1＜x2＜1，则m的取值范围是______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线C：y1＝ax2－ah(2x－h)－2，直线l：y2＝k(x－h)－2．
(1)求证：直线l恒过抛物线C的顶点；
(2)当a＝－1，m≤x≤2时，y1≥x－4恒成立，求m的最小值；
(3)当0＜a≤3，k＞0时，若在直线l下方的抛物线C上至少存在两个横坐标为整数的点，求k的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：
和
均为等腰直角三角形，
，
，
，连接
.
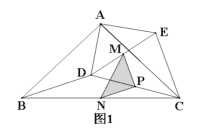
（1）如图1所示，线段
与
的数量关系是_____，位置关系是_____；
（2）在图1中，若点M、P、N分别为
的中点，连接
，请判断
的形状，并说明理由；
（3）如图2所示，若M、N、P分别为
上的点，且满足
，
，连接，则线段
长度是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线
经过点
和点
，与
轴交于点
.
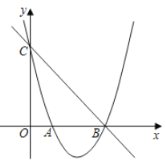
（1）求此抛物线的解析式；
（2）若点
是直线
下方的抛物线上一动点（不点
，重合），过点作轴的平行线交直线于点
，设点的横坐标为
.
①用含的代数式表示线段
的长；
②连接
，
，求
的面积最大时点的坐标；
（3）设抛物线的对称轴与交于点
，点
是抛物线的对称轴上一点，
为轴上一点，是否存在这样的点和点，使得以点、、、为顶点的四边形是菱形？如果存在，请直接写出点的坐标；如果不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
