
【题目】已知:![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.
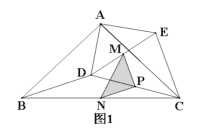

(1)如图1所示,线段![]() 与
与![]() 的数量关系是_____,位置关系是_____;
的数量关系是_____,位置关系是_____;
(2)在图1中,若点M、P、N分别为![]() 的中点,连接
的中点,连接![]() ,请判断
,请判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)如图2所示,若M、N、P分别为![]() 上的点,且满足
上的点,且满足![]() ,
,![]() ,连接
,连接![]() ,则线段
,则线段![]() 长度是多少?
长度是多少?
【答案】(1)相等,垂直;(2)![]() 为等腰直角三角形,证明见解析;(3)
为等腰直角三角形,证明见解析;(3)![]() .
.
【解析】
(1)延长BD与EC相交于F,证明△ABD≌△ACE,根据全等三角形的性质可得BD=CE,![]() ,再进一步证明
,再进一步证明![]() 可得∠BFC=90°,由此可证明
可得∠BFC=90°,由此可证明![]() 与
与![]() 垂直且相等;
垂直且相等;
(2)结合(1),根据中位线的定理,可推出![]() 为等腰直角三角形;
为等腰直角三角形;
(3)证明△CPN∽△CDB,△DPM∽△DCE,根据相似三角形的性质可求得NP和MP的值,结合(2)可证明∠NPM=90°,根据勾股定理可求得MN的长度.
解:(1)如下图延长BD与EC相交于F,
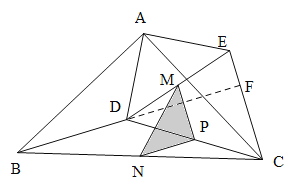
∵![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,
∴![]()
∴![]()
又∵![]() ,
,![]()
∴△ABD≌△ACE(SAS)
∴BD=CE,![]() ,
,
∵![]()
∴![]() ,
,
∴ ![]()
∴![]() ,即
,即![]()
∴![]() ,即
,即![]() .
.
故线段![]() 与
与![]() 的数量关系是相等,位置关系是垂直.答案为:相等,垂直.
的数量关系是相等,位置关系是垂直.答案为:相等,垂直.
(2)![]() 为等腰直角三角形,理由如下:
为等腰直角三角形,理由如下:
∵点M、P、N分别为![]() 的中点,
的中点,
∴NP和MP分别为△BCD和△ECD的中位线,
∴![]()
∴![]() ,
,
由(1)得BD=CE,
∴![]() ,
,
由(1)得![]() ,
,
∴![]()
∴![]() ,即
,即![]() .
.
∴![]() 为等腰直角三角形.
为等腰直角三角形.
(3)∵![]()
∴![]()
又∵∠BCD=∠BCD
∴△CPN∽△CDB
∴![]() ,
,![]() ,
,
∴NP//BD,
∵![]()
∴![]() ,
,
同理可证△DPM∽△DCE,![]() ,MP//EC,
,MP//EC,
∴![]()
与(2)同理可证![]() ,
,
∴在Rt△![]() 中,根据勾股定理
中,根据勾股定理
![]() .
.


科目:初中数学 来源: 题型:
【题目】某兴趣小组为了解我市气温变化情况,记录了今年月份连续![]() 天的最低气温(单位:℃):
天的最低气温(单位:℃):![]() .关于这组数据,下列结论不正确的是( )
.关于这组数据,下列结论不正确的是( )
A.平均数是![]() B.中位数是
B.中位数是![]() C.众数是
C.众数是![]() D.方差是
D.方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
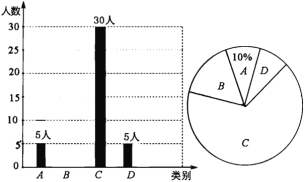
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____________人,扇形统计图中C部分所对应的扇形圆心角的度数为_______.
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有__________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平不断提高,我市 “初中生带手机”现象也越来越多,为了了解家长对此现象的态度,某校数学课外活动小组随机调查了若干名学生家长,并将调查结果进行统计,得出如下所示的条形统计图和扇形统计图.
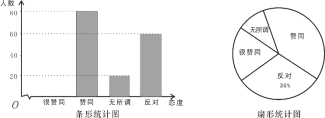
问 (1)这次调查的学生家长总人数为 .
(2)请补全条形统计图,并求出持“很赞同”态度的学生家长占被调查总人数的百分比.
(3)求扇形统计图中表示学生家长持“无所谓”态度的扇形圆心角的度数.
(4)该校共有学生1200人,求赞同的家长的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD、BD分别是![]() 的内角∠BAC、∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E.
的内角∠BAC、∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E.

(1)求证:![]() ;
;
(2)如图2,如果AE=AB,且BD:DE=2:3,求BC:AB的值;
(3)如果∠ABC是锐角,且![]() 与
与![]() 相似,求∠ABC的度数,并直接写出
相似,求∠ABC的度数,并直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
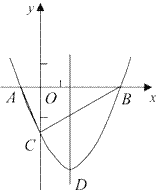
【题目】如图,抛物线y=![]() x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
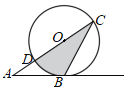
【题目】如图,⊙O的圆心O在△ABC的边AC上,AC与⊙O分别交于C,D两点,⊙O与边AB相切,且切点恰为点B.
(1)求证:∠A+2∠C=90°;
(2)若∠A=30°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商业集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(单位:元)如下表:
空调机 | 电冰箱 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店![]() 台空调机,集团卖出这100台电器的总利润为
台空调机,集团卖出这100台电器的总利润为![]() (元).
(元).
(1)求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利![]() 元销售,其他的销售利润都不变,并且让利后每台空调机的利润比甲连锁店销售每台电冰箱的利润至少高出10元,问该集团应该如何设计调配方案,能使总利润达到最大.
元销售,其他的销售利润都不变,并且让利后每台空调机的利润比甲连锁店销售每台电冰箱的利润至少高出10元,问该集团应该如何设计调配方案,能使总利润达到最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=-x2+bx+c的图像与x轴的交点为点A(3,0)和点B,与y轴交于点C(0,3),连接AC.
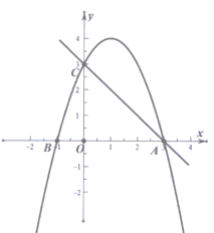
(1)求这个二次函数的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△ACD的面积最大?若存在,求出点D的坐标及△ACD面积的最大值,若不存在,请说明理由.
(3)在抛物线上是否存在点E,使得△ACE是以AC为直角边的直角三角形如果存在,请直接写出点E的坐标即可;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com