
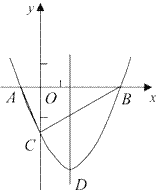
【题目】如图,抛物线y=![]() x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
【答案】(1)抛物线的解析式为y=![]() x2-
x2-![]() x-2
x-2
顶点D的坐标为 (![]() , -
, -![]() ).
).
(2)△ABC是直角三角形,理由见解析;
(3)![]() .
.
【解析】
(1)把点A坐标代入抛物线即可得解析式,从而求得顶点坐标;
(2)分别计算出三条边的长度,符合勾股定理可知其是直角三角形;
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC + MD的值最小.
解:(1)∵点A(-1,0)在抛物线y=![]() x2 +bx-2上
x2 +bx-2上
∴![]() × (-1 )2 +b× (-1) –2 = 0
× (-1 )2 +b× (-1) –2 = 0
解得b =![]()
∴抛物线的解析式为y=![]() x2-
x2-![]() x-2.
x-2.
y=![]() x2-
x2-![]() x-2 =
x-2 =![]() (x2 -3x- 4 ) =
(x2 -3x- 4 ) =![]() (x-
(x-![]() )2-
)2-![]() ,
,
∴顶点D的坐标为 (![]() , -
, -![]() ).
).
(2)当x = 0时y = -2,
∴C(0,-2),OC = 2.
当y = 0时,![]() x2-
x2-![]() x-2 = 0, ∴x1 = -1, x2 = 4
x-2 = 0, ∴x1 = -1, x2 = 4
∴B (4,0)
∴OA =1, OB = 4, AB = 5.
∵AB2 = 25, AC2 =OA2 +OC2 = 5, BC2 =OC2 +OB2 = 20,
∴AC2 +BC2 =AB2.
∴△ABC是直角三角形.
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC +MD的值最小.

解法一:设抛物线的对称轴交x轴于点E.
∵ED∥y轴, ∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴![]()
∴ ,∴m=
,∴m=![]() .
.
解法二:设直线C′D的解析式为y =kx +n ,
则 ,解得n = 2,
,解得n = 2,![]() .
.
∴![]() .
.
∴当y = 0时,![]() ,
,
![]()
∴![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
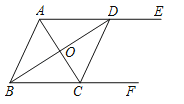
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②a﹣b+c<0;③4a+b+c=0;④抛物线的顶点坐标为(2,b);⑤当x<1时,y随x增大而增大.其中结论正确的是( )
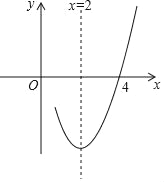
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,点
中,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,根据下列给定的条件,不能判断
上,根据下列给定的条件,不能判断![]() 与
与![]() 平行的是( )
平行的是( )
A. AD=6,BD=4,AE=2.4,CE=1.6
B. BD=2,AB=6,CE=1,AC=3;
C. AD=4,AB=6,DE=2,BC=3;
D. AD=4,AB=6,AE=2,AC=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.
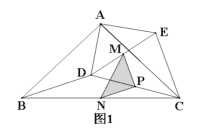

(1)如图1所示,线段![]() 与
与![]() 的数量关系是_____,位置关系是_____;
的数量关系是_____,位置关系是_____;
(2)在图1中,若点M、P、N分别为![]() 的中点,连接
的中点,连接![]() ,请判断
,请判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)如图2所示,若M、N、P分别为![]() 上的点,且满足
上的点,且满足![]() ,
,![]() ,连接
,连接![]() ,则线段
,则线段![]() 长度是多少?
长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控.甲、乙两个工厂生产同一种防护口罩,甲厂每天比乙厂多生产口罩5万只,甲厂生产该种口罩40万只所用时间与乙厂生产该种口罩15万只所用时间相同,甲、乙两个工厂每天分别生产该种口罩多少万只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近些年来,“校园安全”受到全社会的广泛关注,为了了解学生对于安全知识的了解程度,学校采用随机抽样的调查方式,根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.
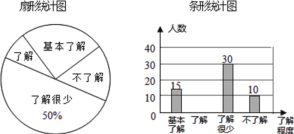
请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有________人.
(2)请补全条形统计图;
(3)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与直线y=﹣x﹣2相交于A(﹣2,0),B(m,﹣6)两点,且抛物线经过点C (5,0).点P是直线下方的抛物线上异于A、B的动点.过点P作PD⊥x轴于点D,交直线于点E.
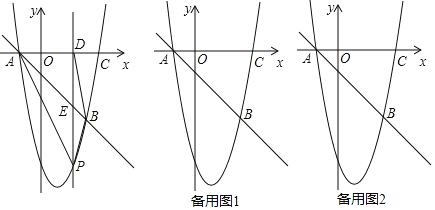
(1)求抛物线的解析式;
(2)连结PA、PB、BD,当S△ADB![]() S△PAB时,求S△PAB;
S△PAB时,求S△PAB;
(3)是否存在点P,使得△PBE为直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.已知:在矩形![]() 中,
中,![]() 是对角线,
是对角线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ;
;
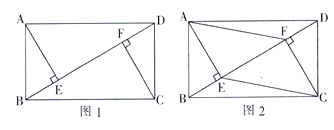
(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,连接
时,连接![]() .
.![]() ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形![]() 面积的
面积的![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com