
【题目】如图,抛物线y=ax2+bx+c(a≠0)与直线y=﹣x﹣2相交于A(﹣2,0),B(m,﹣6)两点,且抛物线经过点C (5,0).点P是直线下方的抛物线上异于A、B的动点.过点P作PD⊥x轴于点D,交直线于点E.
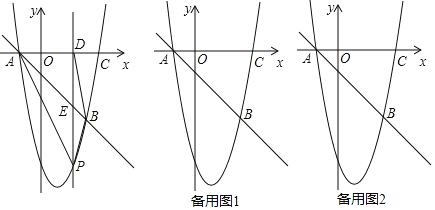
(1)求抛物线的解析式;
(2)连结PA、PB、BD,当S△ADB![]() S△PAB时,求S△PAB;
S△PAB时,求S△PAB;
(3)是否存在点P,使得△PBE为直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
【答案】(1)y=x2﹣3x﹣10;(2)S△PAB=![]() ;(3)存在,满足条件点P的坐标为(0,﹣10)或(﹣1,6).
;(3)存在,满足条件点P的坐标为(0,﹣10)或(﹣1,6).
【解析】
(1)因为抛物线经过A(-2,0),C(5,0),可以假设抛物线的解析式y=a(x+2)(x-5),把B(4,-6)代入y=a(x+2)(x-5),可得a=1解决问题;
(2)设P(x,x2-3x-10),根据S△ADB![]() S△PAB,构建方程解决问题即可;
S△PAB,构建方程解决问题即可;
(3)分两种情形:①∠PBE=90°.②∠BPE=90°.分别求解即可解决问题.
(1)将B(m,﹣6)代入y=﹣x﹣2得-6=﹣m﹣2,解得m=4 ,
∴B(4,﹣6),
∵抛物线经过A(﹣2,0),C(5,0),
∴可以假设抛物线的解析式y=a(x+2)(x﹣5),
把B(4,﹣6)代入y=a(x+2)(x﹣5),可得a=1,
∴抛物线的解析式为y=x2﹣3x﹣10.
(2)设P(x,x2﹣3x﹣10),
∵直线AB的解析式为y=﹣x﹣2,
∴D(x,0),E(x,﹣x﹣2),
∴PE=﹣x2+2x+8,
∵S△ADB═![]() S△PAB,
S△PAB,
∴![]() ×(x+2)×6=
×(x+2)×6=![]() ×
×![]() ×(﹣x2+2x+8)×6,
×(﹣x2+2x+8)×6,
整理得:2x2﹣x﹣10=0,
解得x=![]() 或﹣2(舍去).
或﹣2(舍去).
∴PE=![]() ,
,
∴S△PAB=![]() ×6×
×6×![]() =
=![]() .
.
(3)①当∠PBE=90°时,PB⊥AB,
∴设直线PB的解析式y=x﹣b,
将B(4,﹣6)代入解得b=10,
∴直线PB的解析式y=x﹣10,
由 ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
∴p(0,﹣10).
②当∠BPE=90°时,PB∥x轴,
由﹣6=x2﹣3x﹣10,解得x=4(舍去)或﹣1,
∴p(﹣1,6),
综上所述,满足条件点P的坐标为(0,﹣10)或(﹣1,6).


科目:初中数学 来源: 题型:
【题目】问题情境:在综合实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图(1),将一张菱形纸片ABCD(∠BAD=60°)沿对角线AC剪开,得到△ABC和△ACD
操作发现:(1)将图(1)中的△ABC以A为旋转中心,顺时针方向旋转角α(0°<α<60°)得到如图(2)所示△ABC′,分别延长BC′和DC交于点E,发现CE=C′E.请你证明这个结论.
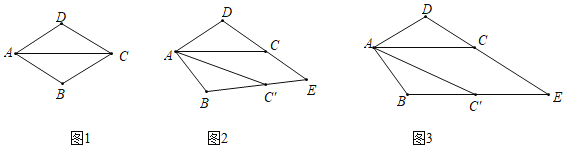
(2)在问题(1)的基础上,当旋转角α等于多少度时,四边形ACEC′是菱形?请你利用图(3)说明理由.
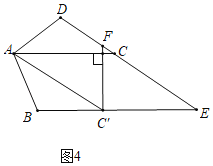
拓展探究:(3)在满足问题(2)的基础上,过点C′作C′F⊥AC,与DC交于点F.试判断AD、DF与AC的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
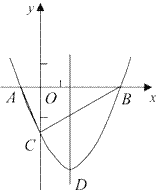
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)求y与x之间的函数关系式.
(2)由于湖北省武汉市爆发了新型冠状病毒肺炎(简称“新冠肺炎”)疫情,该网店店主决定从每天获得的利润中抽出200元捐献给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定这款电动牙刷的销售单价?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商业集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(单位:元)如下表:
空调机 | 电冰箱 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店![]() 台空调机,集团卖出这100台电器的总利润为
台空调机,集团卖出这100台电器的总利润为![]() (元).
(元).
(1)求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利![]() 元销售,其他的销售利润都不变,并且让利后每台空调机的利润比甲连锁店销售每台电冰箱的利润至少高出10元,问该集团应该如何设计调配方案,能使总利润达到最大.
元销售,其他的销售利润都不变,并且让利后每台空调机的利润比甲连锁店销售每台电冰箱的利润至少高出10元,问该集团应该如何设计调配方案,能使总利润达到最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在A处的正东方向有一港口B.某巡艇从A处沿着北偏东60°方向巡逻,到达C处时接到命令,立刻在C处沿东南方向以20海里/小时的速度行驶3小时到达港口B.若取![]()
![]() 结果保留一位小数,则A,B间的距离为()
结果保留一位小数,则A,B间的距离为()
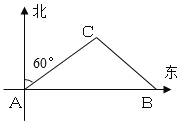
A.42.3海里B.73.5海里C.115.8海里D.119.9海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,点E、F分别为正方形ABCD的边BC、CD上一点,AC、BD交于点O,且∠EAF=45°,AE,AF分别交对角线BD于点M,N,则有以下结论:①△AOM∽△ADF;②EF=BE+DF;③∠AEB=∠AEF=∠ANM;④S△AEF=2S△AMN,以上结论中,正确的个数有( )个.
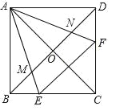
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=![]() (k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
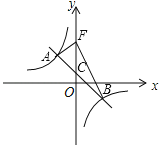
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com