
【题目】问题情境:在综合实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图(1),将一张菱形纸片ABCD(∠BAD=60°)沿对角线AC剪开,得到△ABC和△ACD
操作发现:(1)将图(1)中的△ABC以A为旋转中心,顺时针方向旋转角α(0°<α<60°)得到如图(2)所示△ABC′,分别延长BC′和DC交于点E,发现CE=C′E.请你证明这个结论.
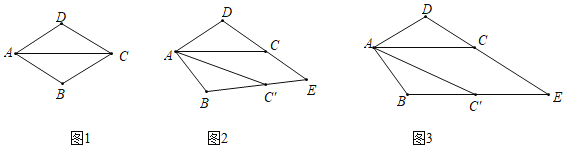
(2)在问题(1)的基础上,当旋转角α等于多少度时,四边形ACEC′是菱形?请你利用图(3)说明理由.
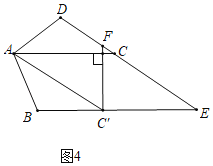
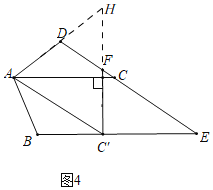
拓展探究:(3)在满足问题(2)的基础上,过点C′作C′F⊥AC,与DC交于点F.试判断AD、DF与AC的数量关系,并说明理由.
【答案】(1)见解析;(2)当α=30°时,四边形AC′EC是菱形,理由见解析;(3)AD+DF=AC,理由见解析
【解析】
(1)先判断出∠ACC′=∠AC′C,进而判断出∠ECC′=∠EC′C,即可得出结论;
(2)判断出四边形AC′EC是平行四边形,即可得出结论;
(3)先判断出HAC′是等边三角形,得出AH=AC′,∠H=60°,再判断出△HDF是等边三角形,即可得出结论.
(1)证明:如图2,连接CC′,
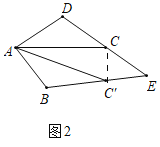
∵四边形ABCD是菱形,
∴∠ACD=∠AC′B=30°,AC=AC′,
∴∠ACC′=∠AC′C,
∴∠ECC′=∠EC′C,
∴CE=C′E;
(2)当α=30°时,四边形AC′EC是菱形,
理由:∵∠DCA=∠CAC′=∠AC′B=30°,
∴CE∥AC′,AC∥C′E,
∴四边形AC′EC是平行四边形,
又∵CE=C′E,
∴四边形AC′EC是菱形;
(3)AD+DF=AC.
理由:如图4,分别延长CF与AD交于点H,
∵∠DAC=∠C′AC=30°,C′F⊥AC,
∴∠AC′H=∠DAC′=60°,
∴△HAC′是等边三角形,
∴AH=AC′,∠H=60°,
又∵AD=DC,
∴∠DAC=∠DCA=30°,
∴∠HDC=∠DAC+∠DCA=60°,
∴△HDF是等边三角形,
∴DH=DF,
∴AD+DF=AD+DH=AH.
∵AC′=AC,
∴AC=AD+DF.


科目:初中数学 来源: 题型:
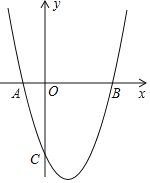
【题目】如图,已知二次函数y=x2﹣2x+m的图象与x轴交于点A、B,与y轴交于点C,直线AC交二次函数图象的对称轴于点D,若点C为AD的中点.
(1)求m的值;
(2)若二次函数图象上有一点Q,使得tan∠ABQ=3,求点Q的坐标;
(3)对于(2)中的Q点,在二次函数图象上是否存在点P,使得△QBP∽△COA?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
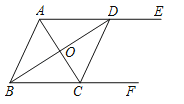
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
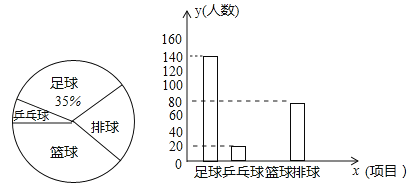
【题目】某校为提高学生身体素质,决定开展足球、篮球、台球、乒乓球四项课外体育活动,并要求学生必须并且只能选择一项.为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并绘制出以下两幅不完整的统计图.请根据统计图回答下列问题.(要求写出简要的解答过程)
(1)这次活动一共调查了多少名学生?
(2)补全条形统计图.
(3)若该学校总人数是1300人,请估计选择篮球项目的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②a﹣b+c<0;③4a+b+c=0;④抛物线的顶点坐标为(2,b);⑤当x<1时,y随x增大而增大.其中结论正确的是( )
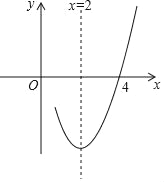
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,点
中,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,根据下列给定的条件,不能判断
上,根据下列给定的条件,不能判断![]() 与
与![]() 平行的是( )
平行的是( )
A. AD=6,BD=4,AE=2.4,CE=1.6
B. BD=2,AB=6,CE=1,AC=3;
C. AD=4,AB=6,DE=2,BC=3;
D. AD=4,AB=6,AE=2,AC=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与直线y=﹣x﹣2相交于A(﹣2,0),B(m,﹣6)两点,且抛物线经过点C (5,0).点P是直线下方的抛物线上异于A、B的动点.过点P作PD⊥x轴于点D,交直线于点E.
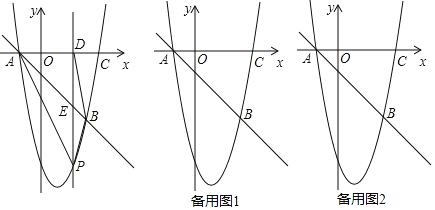
(1)求抛物线的解析式;
(2)连结PA、PB、BD,当S△ADB![]() S△PAB时,求S△PAB;
S△PAB时,求S△PAB;
(3)是否存在点P,使得△PBE为直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com