
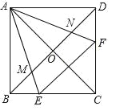
【题目】 如图,点E、F分别为正方形ABCD的边BC、CD上一点,AC、BD交于点O,且∠EAF=45°,AE,AF分别交对角线BD于点M,N,则有以下结论:①△AOM∽△ADF;②EF=BE+DF;③∠AEB=∠AEF=∠ANM;④S△AEF=2S△AMN,以上结论中,正确的个数有( )个.
A. 1B. 2C. 3D. 4
【答案】D
【解析】
如图,把△ADF绕点A顺时针旋转90°得到△ABH,由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,由已知条件得到∠EAH=∠EAF=45°,根据全等三角形的性质得到EH=EF,所以∠ANM=∠AEB,则可求得②正确;
根据三角形的外角的性质得到①正确;
根据相似三角形的判定定理得到△OAM∽△DAF,故③正确;
根据相似三角形的性质得到∠AEN=∠ABD=45°,推出△AEN是等腰直角三角形,根据勾股定理得到AE=![]() AN,再根据相似三角形的性质得到EF=
AN,再根据相似三角形的性质得到EF=![]() MN,于是得到S△AEF=2S△AMN.故④正确.
MN,于是得到S△AEF=2S△AMN.故④正确.
如图,把△ADF绕点A顺时针旋转90°得到△ABH

由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF
∵∠EAF=45°
∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°﹣∠EAF=45°
∴∠EAH=∠EAF=45°
在△AEF和△AEH中
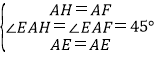
∴△AEF≌△AEH(SAS)
∴EH=EF
∴∠AEB=∠AEF
∴BE+BH=BE+DF=EF,
故②正确
∵∠ANM=∠ADB+∠DAN=45°+∠DAN,
∠AEB=90°﹣∠BAE=90°﹣(∠HAE﹣∠BAH)=90°﹣(45°﹣∠BAH)=45°+∠BAH
∴∠ANM=∠AEB
∴∠ANM=∠AEB=∠ANM;
故③正确,
∵AC⊥BD
∴∠AOM=∠ADF=90°
∵∠MAO=45°﹣∠NAO,∠DAF=45°﹣∠NAO
∴△OAM∽△DAF
故①正确
连接NE,

∵∠MAN=∠MBE=45°,∠AMN=∠BME
∴△AMN∽△BME
∴![]()
∴![]()
∵∠AMB=∠EMN
∴△AMB∽△NME
∴∠AEN=∠ABD=45°
∵∠EAN=45°
∴∠NAE=NEA=45°
∴△AEN是等腰直角三角形
∴AE=![]()
∵△AMN∽△BME,△AFE∽△BME
∴△AMN∽△AFE
∴![]()
∴![]()
∴![]()
∴S△AFE=2S△AMN
故④正确
故选D.


科目:初中数学 来源: 题型:
【题目】我市正大力倡导”垃圾分类“,2015年第一季度某企业按A类垃圾处理费25元/吨、B类垃圾处理费16元/吨的收费标准,共支付垃圾处理费520元.从2015年4月起,收费标准上调为:A类垃圾处理费100元/吨,B类垃圾处理费30元/吨.若该企业2015年第二季度需要处理的A类,B类垃圾的数量与第一季度相同,就要多支付垃圾处理费880元.
(1)该企业第一季度处理的两类垃圾各多少吨?
(2)该企业计划第二季度将上述两种垃圾处理总量减少到24吨,且B类垃圾处理量不超过A类垃圾处理量的3倍,该企业第二季度最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.

(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
(3)点![]() 是
是![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的值最小时,求
的值最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:
.下列结论:
①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8; ④0<CE≤6.4.

其中正确的结论是____________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三个完全相同的小球上分别写上-2,-1,2三个数字,然后装入一个不透明的布袋内搅匀,从布袋中取出一个球,记下小球上的数字为![]() ,放回袋中再搅匀,然后再从袋中取出一个小球,记下小球上的数字为
,放回袋中再搅匀,然后再从袋中取出一个小球,记下小球上的数字为![]() ,组成一对数
,组成一对数![]() .
.
(1)请用列表或画树状图的方法,表示出数对![]() 的所有可能的结果;
的所有可能的结果;
(2)求直线![]() 不经过第一象限的概率.
不经过第一象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形的边长均为1的方格纸中,有线段![]() 和线段
和线段![]() ,点
,点![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
(1)在方格纸中画出以![]() 为斜边的直角三角形
为斜边的直角三角形![]() ,点E在小正方形的顶点上,且
,点E在小正方形的顶点上,且![]() 的面积为5;
的面积为5;
(2)在方格纸中画出以![]() 为一边的
为一边的![]() ,点
,点![]() 在小正方形的顶点上,
在小正方形的顶点上,![]() 的面积为4,射线
的面积为4,射线![]() 与射线
与射线![]() 交于点
交于点![]() ,且
,且![]() ,连接
,连接![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个.若从中任意摸出一个球,它是蓝球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)从袋中一次摸出两个球,请用画树状图或列表格的方法列出所有等可能的结果,并求出摸到两个不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com