
ЁОЬтФПЁПШчЭМЫљЪОЃЌвбжЊЖўДЮКЏЪ§y=-x2+bx+cЕФЭМЯёгыxжсЕФНЛЕуЮЊЕуA(3ЃЌ0)КЭЕуBЃЌгыyжсНЛгкЕуC(0ЃЌ3)ЃЌСЌНгAC.
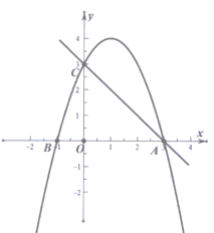
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдк(1)жаЮЛгкЕквЛЯѓЯоФкЕФХзЮяЯпЩЯЪЧЗёДцдкЕуDЃЌЪЙЕУЁїACDЕФУцЛ§зюДѓ?ШєДцдкЃЌЧѓГіЕуDЕФзјБъМАЁїACDУцЛ§ЕФзюДѓжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЃЈ3ЃЉдкХзЮяЯпЩЯЪЧЗёДцдкЕуEЃЌЪЙЕУЁїACEЪЧвдACЮЊжБНЧБпЕФжБНЧШ§НЧаЮШчЙћДцдкЃЌЧыжБНгаДГіЕуEЕФзјБъМДПЩЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉy=-x2+2x+3ЃЛЃЈ2ЃЉХзЮяЯпЩЯДцдкЕуDЃЌЪЙЕУЁїACDЕФУцЛ§зюДѓЃЌДЫЪБЕуDЕФзјБъЮЊ( ![]() ЃЌ
ЃЌ ![]() )ЧвЁїACDУцЛ§ЕФзюДѓжЕ
)ЧвЁїACDУцЛ§ЕФзюДѓжЕ ![]() ЃЛЃЈ3ЃЉдкХзЮяЯпЩЯДцдкЕуEЃЌЪЙЕУЁїACEЪЧвдACЮЊжБНЧБпЕФжБНЧШ§НЧаЮ
ЃЛЃЈ3ЃЉдкХзЮяЯпЩЯДцдкЕуEЃЌЪЙЕУЁїACEЪЧвдACЮЊжБНЧБпЕФжБНЧШ§НЧаЮ
ЕуEЕФзјБъЪЧ(1ЃЌ4)Лђ(-2ЃЌ-5).
ЁОНтЮіЁП
(1)вђЮЊЕуA(3ЃЌ0)ЃЌЕуC(0,3)дкХзЮяЯпy=x2+bx+cЩЯЃЌПЩДњШыШЗЖЈbЁЂcЕФжЕЃЛ
(2)Й§ЕуDзїDHЁЭxжсЃЌЩшD(tЃЌ-t2+2t+3)ЃЌЯШРћгУЭМЯѓЩЯЕуЕФЬиеїБэЪОГіSЁїACD=SЬнаЮOCDH+SЁїAHD-SЁїAOC=![]() ЃЌдйРћгУЖЅЕузјБъЧѓзюжЕМДПЩЃЛ
ЃЌдйРћгУЖЅЕузјБъЧѓзюжЕМДПЩЃЛ
(3)ЗжСНжжЧщПіЬжТлЃКЂйЙ§ЕуAзїAE1ЁЭACЃЌНЛХзЮяЯпгкЕуE1ЃЌНЛyжсгкЕуFЃЌСЌНгE1CЃЌЧѓГіЕуFЕФзјБъЃЌдйЧѓжБЯпAEЕФНтЮіЪНЮЊyЃНx3ЃЌдйгыЖўДЮКЏЪ§ЕФНтЮіЪНСЊСЂЗНГЬзщЧѓНтМДПЩЃЛЂкЙ§ЕуCзїCEЁЭCAЃЌНЛХзЮяЯпгкЕуE2ЁЂНЛxжсгкЕуMЃЌСЌНгAE2ЃЌЧѓГіжБЯпCMЕФНтЮіЪНЮЊyЃНxЃЋ3ЃЌдйгыЖўДЮКЏЪ§ЕФНтЮіЪНСЊСЂЗНГЬзщЧѓНтМДПЩ.
ЃЈ1ЃЉНтЃКЁпЖўДЮКЏЪ§y=-x2+bx+cгыxжсЕФНЛЕуЮЊЕуA(3ЃЌ0)гыyжсНЛгкЕуC(0ЃЌ3)
Ёр![]()
НтжЎЕУ ![]()
ЁретИіЖўДЮКЏЪ§ЕФНтЮіЪНЮЊy=-x2+2x+3
ЃЈ2ЃЉНтЃКШчЭМЃЌЩшD(tЃЌ-t2+2t+3)ЃЌЙ§ЕуDзїDHЁЭxжсЃЌДЙзуЮЊHЃЌ
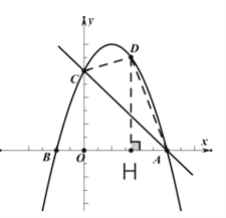
дђSЁїACD=SЬнаЮOCDH+SЁїAHD-SЁїAOC
= ![]() (-t2+2t+3+3)+
(-t2+2t+3+3)+ ![]() (3-t)(-t2+2t+3)-
(3-t)(-t2+2t+3)- ![]() ЁС3ЁС3
ЁС3ЁС3
= ![]()
= ![]()
Ёп ![]() <0
<0
ЁрЕБt= ![]() ЪБЃЌЁїACDЕФУцЛ§газюДѓжЕ
ЪБЃЌЁїACDЕФУцЛ§газюДѓжЕ ![]()
ДЫЪБ-t2+2t+3= ![]()
ЁрХзЮяЯпЩЯДцдкЕуDЃЌЪЙЕУЁїACDЕФУцЛ§зюДѓЃЌДЫЪБЕуDЕФзјБъЮЊ( ![]() ЃЌ
ЃЌ ![]() )ЧвЁїACDУцЛ§ЕФзюДѓжЕ
)ЧвЁїACDУцЛ§ЕФзюДѓжЕ ![]()
ЃЈ3ЃЉдкХзЮяЯпЩЯДцдкЕуEЃЌЪЙЕУЁїACEЪЧвдACЮЊжБНЧБпЕФжБНЧШ§НЧаЮ
ЕуEЕФзјБъЪЧ(1ЃЌ4)Лђ(-2ЃЌ-5).
РэгЩШчЯТЃКгаСНжжЧщПіЃК
ЂйШчЭМЃЌ

Й§ЕуAзїAE1ЁЭACЃЌНЛХзЮяЯпгкЕуE1ЁЂНЛyжсгкЕуFЃЌСЌНгE1CЃЎ
ЁпCOЃНAOЃН3ЃЌ
ЁрЁЯCAOЃН45ЁуЃЌ
ЁрЁЯFAOЃН45ЁуЃЌAOЃНOFЃН3ЃЎ
ЁрЕуFЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЎ
ЩшжБЯпAEЕФНтЮіЪНЮЊyЃНkxЃЋbЃЌ
НЋЃЈ0ЃЌ3ЃЉЃЌЃЈ3ЃЌ0ЃЉДњШыyЃНkxЃЋbЕУЃК
![]()
НтЕУ![]()
ЁржБЯпAEЕФНтЮіЪНЮЊyЃНx3ЃЌ
гЩ![]()
НтЕУ![]() Лђ
Лђ![]()
ЁрЕуE1ЕФзјБъЮЊЃЈ2ЃЌ5ЃЉЃЎ
ЂкШчЭМЃЌ

Й§ЕуCзїCEЁЭCAЃЌНЛХзЮяЯпгкЕуE2ЁЂНЛxжсгкЕуMЃЌСЌНгAE2 ЃЎ
ЁпЁЯCAOЃН45ЁуЃЌ
ЁрЁЯCMAЃН45ЁуЃЌOMЃНOCЃН3ЃЎ
ЁрЕуMЕФзјБъЮЊЃЈ3ЃЌ0ЃЉ,
ЩшжБЯпCMЕФНтЮіЪНЮЊyЃНkxЃЋbЃЌ
НЋЃЈ0ЃЌ3ЃЉЃЌЃЈ-3ЃЌ0ЃЉДњШыyЃНkxЃЋbЕУЃК
![]()
НтЕУ![]()
ЁржБЯпCMЕФНтЮіЪНЮЊyЃНxЃЋ3ЃЎ
гЩ![]()
НтЕУЃК![]() Лђ
Лђ![]()
ЁрЕуE2ЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЎ
злЩЯЃЌдкХзЮяЯпЩЯДцдкЕуE1ЃЈ2ЃЌ5ЃЉЁЂE2ЃЈ1ЃЌ4ЃЉЃЌЪЙЁїACE1ЁЂЁїACE2ЪЧвдACЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃК![]() КЭ
КЭ![]() ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() .
.
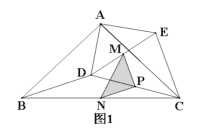

ЃЈ1ЃЉШчЭМ1ЫљЪОЃЌЯпЖЮ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЪЧ_____ЃЌЮЛжУЙиЯЕЪЧ_____ЃЛ
ЕФЪ§СПЙиЯЕЪЧ_____ЃЌЮЛжУЙиЯЕЪЧ_____ЃЛ
ЃЈ2ЃЉдкЭМ1жаЃЌШєЕуMЁЂPЁЂNЗжБ№ЮЊ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЌЧыХаЖЯ
ЃЌЧыХаЖЯ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЫљЪОЃЌШєMЁЂNЁЂPЗжБ№ЮЊ![]() ЩЯЕФЕуЃЌЧвТњзу
ЩЯЕФЕуЃЌЧвТњзу![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌдђЯпЖЮ
ЃЌдђЯпЖЮ![]() ГЄЖШЪЧЖрЩйЃП
ГЄЖШЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ5ЃЌЕуAЕФзјБъЮЊЃЈЉ4ЃЌ0ЃЉЃЌЕуBдкyжсЩЯЃЌШєЗДБШР§КЏЪ§y=![]() ЃЈkЁй0ЃЉЕФЭМЯѓЙ§ЕуCЃЌдђИУЗДБШР§КЏЪ§ЕФБэДяЪНЮЊ_______ЃЎ
ЃЈkЁй0ЃЉЕФЭМЯѓЙ§ЕуCЃЌдђИУЗДБШР§КЏЪ§ЕФБэДяЪНЮЊ_______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
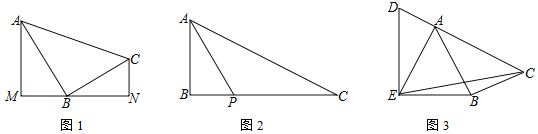
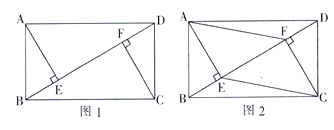
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯABC=90ЁуЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЗжБ№Й§AЁЂCСНЕузїОЙ§ЕуBЕФжБЯпЕФДЙЯпЃЌДЙзуЗжБ№ЮЊMЁЂNЃЌЧѓжЄЃКЁїABMЁзЁїBCNЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌPЪЧБпBCЩЯвЛЕуЃЌЁЯBAP=ЁЯCЃЌtanЁЯPAC=![]() ЃЌЧѓtanCЕФжЕЃЛ
ЃЌЧѓtanCЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌDЪЧБпCAбгГЄЯпЩЯвЛЕуЃЌAE=ABЃЌЁЯDEB=90ЁуЃЌsinЁЯBAC=![]() ЃЌ
ЃЌ![]() ЃЌжБНгаДГіtanЁЯCEBЕФжЕЃЎ
ЃЌжБНгаДГіtanЁЯCEBЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§![]() ЃЈaЃМ0ЃЉЭМЯѓгыxжсЕФНЛЕуAЁЂBЕФКсзјБъЗжБ№ЮЊЉ3ЃЌ1ЃЌгыyжсНЛгкЕуCЃЌЯТУцЫФИіНсТлЃК
ЃЈaЃМ0ЃЉЭМЯѓгыxжсЕФНЛЕуAЁЂBЕФКсзјБъЗжБ№ЮЊЉ3ЃЌ1ЃЌгыyжсНЛгкЕуCЃЌЯТУцЫФИіНсТлЃК
Ђй16aЉ4b+cЃМ0ЃЛЂкШєPЃЈЉ5ЃЌy1ЃЉЃЌQЃЈ![]() ЃЌy2ЃЉЪЧКЏЪ§ЭМЯѓЩЯЕФСНЕуЃЌдђy1ЃОy2ЃЛЂлa=Љ
ЃЌy2ЃЉЪЧКЏЪ§ЭМЯѓЩЯЕФСНЕуЃЌдђy1ЃОy2ЃЛЂлa=Љ![]() cЃЛЂмШєЁїABCЪЧЕШбќШ§НЧаЮЃЌдђb=Љ
cЃЛЂмШєЁїABCЪЧЕШбќШ§НЧаЮЃЌдђb=Љ![]() ЃЎЦфжае§ШЗЕФга______ЃЈЧыНЋНсТле§ШЗЕФађКХШЋВПЬюЩЯЃЉ
ЃЎЦфжае§ШЗЕФга______ЃЈЧыНЋНсТле§ШЗЕФађКХШЋВПЬюЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП.вбжЊЃКдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧЖдНЧЯпЃЌ
ЪЧЖдНЧЯпЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЛ
ЃЛ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБ![]() ЪБЃЌСЌНг
ЪБЃЌСЌНг![]() .
.![]() ЃЌдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЭМ2жаЫФИіШ§НЧаЮЃЌЪЙаДГіЕФУПИіШ§НЧаЮЕФУцЛ§ЖМЕШгкОиаЮ
ЃЌдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЭМ2жаЫФИіШ§НЧаЮЃЌЪЙаДГіЕФУПИіШ§НЧаЮЕФУцЛ§ЖМЕШгкОиаЮ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
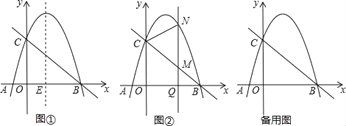
ЁОЬтФПЁПШчЭМЂйвбжЊХзЮяЯпy=ax2Љ3axЉ4aЃЈaЃМ0ЃЉЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЈAдкBЕФзѓВрЃЉЃЌгыyЕФе§АыжсНЛгкЕуCЃЌСЌНсBCЃЌЖўДЮКЏЪ§ЕФЖдГЦжсгыxжсЕФНЛЕуЮЊEЃЎ
ЃЈ1ЃЉХзЮяЯпЕФЖдГЦжсгыxжсЕФНЛЕуEзјБъЮЊ_____ЃЌЕуAЕФзјБъЮЊ_____ЃЛ
ЃЈ2ЃЉШєвдEЮЊдВаФЕФдВгыyжсКЭжБЯпBCЖМЯрЧаЃЌЪдЧѓГіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШчЭМЂкQЃЈmЃЌ0ЃЉЪЧxЕФе§АыжсЩЯвЛЕуЃЌЙ§ЕуQзїyжсЕФЦНааЯпЃЌгыжБЯпBCНЛгкЕуMЃЌгыХзЮяЯпНЛгкЕуNЃЌСЌНсCNЃЌНЋЁїCMNбиCNЗелЃЌMЕФЖдгІЕуЮЊMЁфЃЎдкЭМЂкжаЬНОПЃКЪЧЗёДцдкЕуQЃЌЪЙЕУMЁфЧЁКУТфдкyжсЩЯЃПШєДцдкЃЌЧыЧѓГіQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
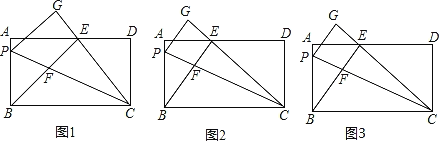
ЁОЬтФПЁПдкОиаЮABCDжаЃЌABЃН12ЃЌPЪЧБпABЩЯвЛЕуЃЌАбЁїPBCбижБЯпPCелЕўЃЌЖЅЕуBЕФЖдгІЕуЪЧЕуGЃЌЙ§ЕуBзїBEЁЭCGЃЌДЙзуЮЊEЧвдкADЩЯЃЌBEНЛPCгкЕуFЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєЕуEЪЧADЕФжаЕуЃЌЧѓжЄЃКЁїAEBЁеЁїDECЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБADЃН25ЃЌЧвAEЃМDEЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕБBEEFЃН108ЪБЃЌЧѓBPЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПга4еХЯрЭЌЕФПЈЦЌЃЌЩЯУцЗжБ№аДгаЪ§зж1ЁЂ2ЁЂ3ЁЂ5ЃЌНЋПЈЦЌЯДдШКѓБГУцГЏЩЯЃЎ
(1)ДгжаШЮвтГщШЁ1еХЃЌГщЕУЕФПЈЦЌЩЯЪ§зжЮЊЦцЪ§ЕФИХТЪЪЧ_______ЃЛ
(2)ДгжаШЮвтГщШЁ1еХЃЌАбЩЯУцЕФЪ§зжзїЮЊЪЎЮЛЪ§ЃЌМЧТМКѓВЛЗХЛиЃЌдйШЮвтГщШЁ1еХАбЩЯУцЕФЪ§зжзїЮЊИіЮЛЪ§ЃЌЧѓзщГЩЕФСНЮЛЪ§ЪЧ3ЕФБЖЪ§ЕФИХТЪЃЎ(гУЪїзДЭМЛђСаБэЕФЗНЗЈ)
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com