
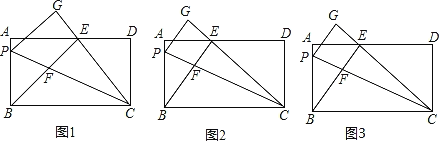
【题目】在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.
(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;
(2)如图2,当AD=25,且AE<DE时,求![]() 的值;
的值;
(3)如图3,当BEEF=108时,求BP的值.
【答案】(1)证明见解析;(2)![]() ;(3)9.
;(3)9.
【解析】
(1)先判断出∠A=∠D=90°,AB=DC,再判断出AE=DE,即可得出结论;
(2)利用折叠的性质,得出∠PGC=∠PBC=90°,∠BPC=∠GPC,进而判断出∠GPF=∠PFB,得出BP=BF,证明![]() ∽
∽![]() ,得出比例式建立方程求解即可得出
,得出比例式建立方程求解即可得出![]() ,再判断出
,再判断出![]() ,进而求出PB,即可得出结论;
,进而求出PB,即可得出结论;
(3)判断出![]() ,得出
,得出![]() ,即可得出结论.
,即可得出结论.
解:(1)在矩形ABCD中,∠A=∠D=90°,AB=DC,
∵E是AD中点,
∴AE=DE,
在△AEB和△DEC中,
 ,
,
∴△AEB≌△DEC(SAS);
(2)在矩形ABCD,∠ABC=90°,
∵△BPC沿PC折叠得到△GPC,
∴∠PGC=∠PBC=90°,∠BPC=∠GPC,
∵BE⊥CG,
∴BE∥PG,
∴∠GPF=∠PFB,
∴∠BPF=∠BFP,
∴BP=BF;
∵∠BEC=90°,
∴∠AEB+∠CED=90°,
∵∠AEB+∠ABE=90°,
∴∠CED=∠ABE,
∵∠A=∠D=90°,
∴△ABE∽△DEC,
∴![]() ,
,
设AE=x,
∴DE=25﹣x,
∴![]() ,
,
∴x=9或x=16,
∵AE<DE,
∴AE=9,DE=16,
∴CE=20,BE=15,
由折叠得,BP=PG,
∴BP=BF=PG,
∵BE∥PG,
∴△ECF∽△GCP,
∴![]() ,
,
设BP=BF=PG=y,
∴![]() ,
,
∴y=![]() ,
,
∴BP=![]() ,
,
∴EF=BE﹣BF=15﹣![]() ,
,
∴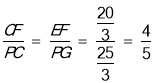 .
.
(3)如图,连接FG,
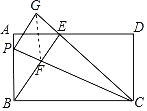
∵∠GEF=∠PGC=90°,
∴∠GEF+∠PGC=180°,
∴BF∥PG
∵BF=PG,
∴BPGF是菱形,
∴BP∥GF,
∴∠GFE=∠ABE,
∴△GEF∽△EAB,
∴![]() ,
,
∴BEEF=ABGF,
∵BEEF=108,AB=12,
∴GF=9,
∴BP=GF=9.


科目:初中数学 来源: 题型:
【题目】某商业集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(单位:元)如下表:
空调机 | 电冰箱 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店![]() 台空调机,集团卖出这100台电器的总利润为
台空调机,集团卖出这100台电器的总利润为![]() (元).
(元).
(1)求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利![]() 元销售,其他的销售利润都不变,并且让利后每台空调机的利润比甲连锁店销售每台电冰箱的利润至少高出10元,问该集团应该如何设计调配方案,能使总利润达到最大.
元销售,其他的销售利润都不变,并且让利后每台空调机的利润比甲连锁店销售每台电冰箱的利润至少高出10元,问该集团应该如何设计调配方案,能使总利润达到最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=-x2+bx+c的图像与x轴的交点为点A(3,0)和点B,与y轴交于点C(0,3),连接AC.
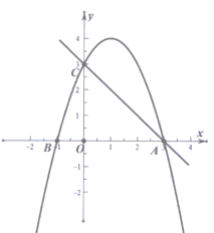
(1)求这个二次函数的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△ACD的面积最大?若存在,求出点D的坐标及△ACD面积的最大值,若不存在,请说明理由.
(3)在抛物线上是否存在点E,使得△ACE是以AC为直角边的直角三角形如果存在,请直接写出点E的坐标即可;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
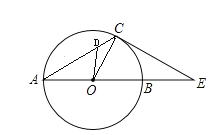
【题目】如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.点D是线段AC上任意一点(不含端点),连接OD,当AB=4时,则![]() CD+OD的最小值是______.
CD+OD的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
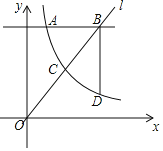
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(1)求反比例函数的解析式;
(2)当BD=2AB时,求点B的坐标;
(3)在(2)的条件下,直接写出不等式![]() >mx的解集.
>mx的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
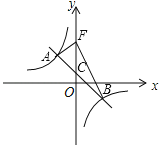
【题目】在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=![]() (k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
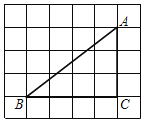
【题目】如图,在6×5的网格(小正方形边长为1)中,Rt△ABC的三个顶点都在格点上.
(1)在网格中,找到格点D,使四边形ACBD的面积为10,并画出这个四边形.
(2)借助网格、只用直尺(无刻度)在AB上找一点E,使△AEC为等腰三角形,且AE=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扫黑除恶”受到广大人民的关注,某中学对部分学生就“扫黑除恶”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“很了解”部分所对应扇形的圆心角为_______;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F分别在边CD、AB上,且满足CE=AF.
(1)求证:△ADE≌△CBF;
(2)连接AC,若AC恰好平分∠EAF,试判断四边形AECF为何种特殊的四边形?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com