
ЁОЬтФПЁПЁАЩЈКкГ§ЖёЁБЪмЕНЙуДѓШЫУёЕФЙизЂЃЌФГжабЇЖдВПЗжбЇЩњОЭЁАЩЈКкГ§ЖёЁБжЊЪЖЕФСЫНтГЬЖШЃЌВЩгУЫцЛњГщбљЕїВщЕФЗНЪНЃЌВЂИљОнЪеМЏЕНЕФаХЯЂНјааЭГМЦЃЌЛцжЦСЫЯТУцСНЗљЩаВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМжаЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК

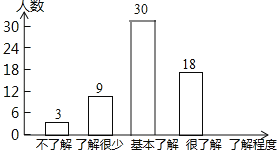
ЃЈ1ЃЉНгЪмЮЪОэЕїВщЕФбЇЩњЙВга_______ШЫЃЌЩШаЮЭГМЦЭМжаЁАКмСЫНтЁБВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЮЊ_______ЃЛ
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєИУжабЇЙВгабЇЩњ900ШЫЃЌЧыИљОнЩЯЪіЕїВщНсЙћЃЌЙРМЦИУжабЇбЇЩњжаЖдЁАЩЈКкГ§ЖёЁБжЊЪЖДяЕНЁАКмСЫНтЁБКЭЁАЛљБОСЫНтЁБГЬЖШЕФзмШЫЪ§.
ЁОД№АИЁПЃЈ1ЃЉ60ЃЌ108ЁуЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉИУжабЇбЇЩњжаЖдаЃдААВШЋжЊЪЖДяЕНЁАКмСЫНтЁБКЭЁАЛљБОСЫНтЁБГЬЖШЕФзмШЫЪ§ЮЊ72ШЫ.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩКмСЫНтЕФга18ШЫЃЌеМ30%ЃЌПЩЧѓЕУНгЪмЮЪОэЕїВщЕФбЇЩњЪ§ЃЌМЬЖјЧѓЕУЩШаЮЭГМЦЭМжаЁАКмСЫНтЁБВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЃЛЃЈ2ЃЉгЩЃЈ1ЃЉПЩЧѓЕУЛљБОСЫНтКмЩйЕФШЫЪ§ЃЌМЬЖјВЙШЋЬѕаЮЭГМЦЭМЃЛЃЈ3ЃЉРћгУбљБОЙРМЦзмЬхЕФЗНЗЈЃЌМДПЩЧѓЕУД№АИ.
ЃЈ1ЃЉНгЪмЮЪОэЕїВщЕФбЇЩњЙВгаЃК18ЁТ30%ЃН60ЃЈШЫЃЉЃЛ
ЁрЩШаЮЭГМЦЭМжаЁАКмСЫНтЁБВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЮЊЃК360ЁуЁС30%ЃН108ЁуЃЛ
ЙЪД№АИЮЊЃК60ЃЌ108ЁуЃЛ
ЃЈ2ЃЉ60Љ3Љ9Љ18ЃН30ЃЛ
ВЙШЋЬѕаЮЭГМЦЭМЕУЃК
ЃЈ3ЃЉИљОнЬтвтЕУЃК900ЁС![]() ЃН720ЃЈШЫЃЉЃЌ
ЃН720ЃЈШЫЃЉЃЌ
дђЙРМЦИУжабЇбЇЩњжаЖдаЃдААВШЋжЊЪЖДяЕНЁАКмСЫНтЁБКЭЁАЛљБОСЫНтЁБГЬЖШЕФзмШЫЪ§ЮЊ72ШЫ.


 бєЙтПЮЬУПЮЪБгХЛЏзївЕЯЕСаД№АИ
бєЙтПЮЬУПЮЪБгХЛЏзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬМвНЋвЛжжЕчЪгЛњАДНјМлЬсИп35%КѓЖЈМлЃЌШЛКѓДђГіЁАОХелГъБіЃЌЭтЫЭ50дЊГізтГЕЗбЁБЕФЙуИцЃЌНсЙћУПЬЈЕчЪгЛњЛёРћ208дЊЃЎ
ЃЈ1ЃЉЧѓУПЬЈЕчЪгЛњЕФНјМлЃЛ
ЃЈ2ЃЉСэгавЛМвЩЬМвГіЪлЭЌРрВњЦЗЃЌАДНјМлЬсИп40%ЃЌШЛКѓДђГіЁААЫелГъБіЁБЕФЙуИцЃЌШчЙћФуЯыТђетжжВњЦЗЃЌгІбЁдёФФвЛИіЩЬМвЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЬнаЮABCDжаЃЌADЁЮBCЃЌAD=6ЃЌBC=16ЃЌEЪЧBCЕФжаЕуЃЎЕуPвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуAГіЗЂЃЌбиADЯђЕуDдЫЖЏЃЛЕуQЭЌЪБвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуCГіЗЂЃЌбиCBЯђЕуBдЫЖЏЃЎЕуPЭЃжЙдЫЖЏЪБЃЌЕуQвВЫцжЎЭЃжЙдЫЖЏЃЎЕБдЫЖЏЪБМф________УыЪБЃЌвдЕуPЃЌQЃЌEЃЌDЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
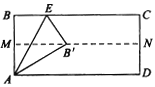
ЁОЬтФПЁПШчЭМЫљЪОЃЌНЋОиаЮABCDжНЖделЃЌЩшелКлЮЊMNЃЌдйАбBЕуЕўдкелКлЯпMNЩЯЃЌЃЈШчЭМЕуBЁЏЃЉЃЌШє![]() ЃЌдђелКлAEЕФГЄЮЊЃЈ ЃЉ
ЃЌдђелКлAEЕФГЄЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() ABCDжаЃЌFЪЧADЕФжаЕуЃЌбгГЄBCЕНЕуEЃЌЪЙCE=
ABCDжаЃЌFЪЧADЕФжаЕуЃЌбгГЄBCЕНЕуEЃЌЪЙCE=![]() BCЃЌСЌНсDEЃЌCFЁЃ
BCЃЌСЌНсDEЃЌCFЁЃ

ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮCEDFЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШєAB=4ЃЌAD=6ЃЌЁЯB=60ЁуЃЌЧѓDEЕФГЄЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГЄЩГЪаТэЭѕЖбЪпВЫХњЗЂЪаГЁФГХњЗЂЩЬдМЦЛЎвдУПЧЇПЫ10дЊЕФЕЅМлЖдЭтХњЗЂЯњЪлФГжжЪпВЫ![]() ЮЊСЫМгПьЯњЪлЃЌИУХњЗЂЩЬЖдМлИёНјааСНДЮЯТЕїКѓЃЌЪлМлНЕЮЊУПЧЇПЫ
ЮЊСЫМгПьЯњЪлЃЌИУХњЗЂЩЬЖдМлИёНјааСНДЮЯТЕїКѓЃЌЪлМлНЕЮЊУПЧЇПЫ![]() дЊЃЎ
дЊЃЎ
![]() ЧѓЦНОљУПДЮЯТЕїЕФАйЗжТЪЃЛ
ЧѓЦНОљУПДЮЯТЕїЕФАйЗжТЪЃЛ
![]() ФГДѓаЭГЌЪазМБИЕНИУХњЗЂЩЬДІЙКТђ2ЖжИУЪпВЫЃЌвђЪ§СПНЯЖрЃЌИУХњЗЂЩЬОіЖЈдйИјгшСНжжгХЛнЗНАИвдЙЉбЁдё
ФГДѓаЭГЌЪазМБИЕНИУХњЗЂЩЬДІЙКТђ2ЖжИУЪпВЫЃЌвђЪ§СПНЯЖрЃЌИУХњЗЂЩЬОіЖЈдйИјгшСНжжгХЛнЗНАИвдЙЉбЁдё![]() ЗНАИвЛЃКДђАЫелЯњЪлЃЛЗНАИЖўЃКВЛДђелЃЌУПЖжгХЛнЯжН№1000дЊ
ЗНАИвЛЃКДђАЫелЯњЪлЃЛЗНАИЖўЃКВЛДђелЃЌУПЖжгХЛнЯжН№1000дЊ![]() ЪдЮЪГЌЪаВЩЙКдБбЁдёФФжжЗНАИИќгХЛнЃПЧыЫЕУїРэгЩЃЎ
ЪдЮЪГЌЪаВЩЙКдБбЁдёФФжжЗНАИИќгХЛнЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпABЁЮCDЃЌжБЯп![]() ЗжБ№НЛ
ЗжБ№НЛ![]() ЃЌ
ЃЌ![]() гк
гк![]() ЃЌ
ЃЌ![]() СНЕуЃЌШє
СНЕуЃЌШє![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЕФНЧЦНЗжЯпЃЌЪдЫЕУїЃКMEЁЮNFЃЎ
ЕФНЧЦНЗжЯпЃЌЪдЫЕУїЃКMEЁЮNFЃЎ
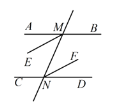
НтЃКЁпABЁЮCDЃЌЃЈвбжЊЃЉ
Ёр![]() ЃЌЃЈ ЃЉ
ЃЌЃЈ ЃЉ
Ёп![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЕФНЧЦНЗжЯпЃЌЃЈвбжЊЃЉ
ЕФНЧЦНЗжЯпЃЌЃЈвбжЊЃЉ
ЁрЁЯEMN= ЁЯAMNЃЌ
ЁЯFNM= ЁЯDNMЃЌЃЈНЧЦНЗжЯпЕФЖЈвхЃЉ
Ёр![]() ЃЌЃЈЕШСПДњЛЛЃЉ
ЃЌЃЈЕШСПДњЛЛЃЉ
ЁрMEЁЮNFЃЌЃЈ ЃЉ
гЩДЫЮвУЧПЩвдЕУГівЛИіНсТлЃКСНЬѕЦНааЯпБЛЕкШ§ЬѕжБЯпЫљНиЃЌвЛЖд НЧЕФЦНЗжЯпЛЅЯр ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ДгЕу
ДгЕу![]() ПЊЪМби
ПЊЪМби![]() БпЯђжеЕу
БпЯђжеЕу![]() вдУПУы
вдУПУы![]() ЕФЫйЖШвЦЖЏЃЌЕу
ЕФЫйЖШвЦЖЏЃЌЕу![]() ДгЕу
ДгЕу![]() ПЊЪМби
ПЊЪМби![]() БпЯђжеЕу
БпЯђжеЕу![]() вдУПУы
вдУПУы![]() ЕФЫйЖШвЦЖЏЃЌЕБЦфжавЛЕуЕНДяжеЕуЪБдЫЖЏЭЃжЙЃЌЩшдЫЖЏЪБМфЮЊ
ЕФЫйЖШвЦЖЏЃЌЕБЦфжавЛЕуЕНДяжеЕуЪБдЫЖЏЭЃжЙЃЌЩшдЫЖЏЪБМфЮЊ![]() Уы.
Уы.
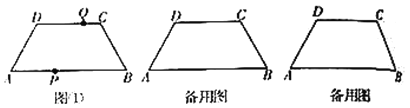
ЃЈ1ЃЉЧѓжЄЃКЕБ![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЛ
ЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌЯпЖЮ
ЮЊКЮжЕЪБЃЌЯпЖЮ![]() ЦНЗжЖдНЧЯп
ЦНЗжЖдНЧЯп![]() ЃПВЂЧѓГіДЫЪБЫФБпаЮ
ЃПВЂЧѓГіДЫЪБЫФБпаЮ![]() ЕФжмГЄЃЛ
ЕФжмГЄЃЛ
ЃЈ3ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌЕу
ЮЊКЮжЕЪБЃЌЕу![]() ЧЁКУдк
ЧЁКУдк![]() ЕФДЙжБЦНЗжЯпЩЯЃП
ЕФДЙжБЦНЗжЯпЩЯЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
![]() ЧѓЪЕЪ§
ЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
![]() ЪЧЗёДцдкЪЕЪ§
ЪЧЗёДцдкЪЕЪ§![]() ЃЌЪЙЗНГЬЕФСНИіЪЕЪ§ИљжЎКЭЕШгкСНЪЕЪ§ИљжЎЛ§ЕФЫуЪѕЦНЗНИљЃПШєДцдкЃЌЧѓГі
ЃЌЪЙЗНГЬЕФСНИіЪЕЪ§ИљжЎКЭЕШгкСНЪЕЪ§ИљжЎЛ§ЕФЫуЪѕЦНЗНИљЃПШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com