
【题目】某商家将一种电视机按进价提高35%后定价,然后打出“九折酬宾,外送50元出租车费”的广告,结果每台电视机获利208元.
(1)求每台电视机的进价;
(2)另有一家商家出售同类产品,按进价提高40%,然后打出“八折酬宾”的广告,如果你想买这种产品,应选择哪一个商家?
科目:初中数学 来源: 题型:
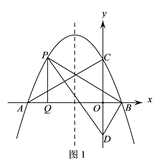
【题目】如图,抛物线y=-![]() x2-
x2-![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-
与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-![]() ).
).
(1)求直线AC的解析式;
(2)如图1,P为直线AC上方抛物线上的一动点,当△PBD的面积最大时,过P作PQ⊥x轴于点Q,M为抛物线对称轴上的一动点,过M作y轴的垂线,垂足为点N,连接PM、NQ,求PM+MN+NQ的最小值;
(3)在(2)问的条件下,将得到的△PBQ沿PB翻折得到△PBQ′,将△PBQ′沿直线BD平移,记平移中的△PBQ′为△P′B′Q″,在平移过程中,设直线P′B′与x轴交于点E,则是否存在这样的点E,使得△B′EQ″为等腰三角形?若存在,求此时OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
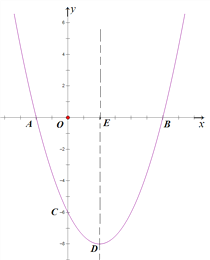
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ=![]() MN时,求菱形对角线MN的长.
MN时,求菱形对角线MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师和小明同学玩数学游戏.老师取出一个不透明的口袋,口袋中装有三张分别标有数字1,2,3的卡片,卡片除数字外其余都相同,老师要求小明同学两次随机抽取一张卡片,并计算两次抽到卡片上的数字之积是奇数的概率.于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果.如图是小明同学所画的正确树状图的一部分.
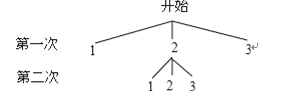
(1)补全小明同学所画的树状图;
(2)求小明同学两次抽到卡片上的数字之积是奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A, 0, B在同一条直线上,OD平分∠AOC, OE平分∠BOC.
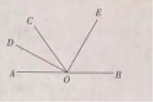
(1)若∠B0D=160°,求∠BOE的度数;
(2) 若∠COE比∠COD多60°.求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
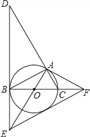
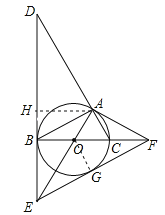
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
(1)求证:△ACF∽△DAE;
(2)若S△AOC=![]() ,求DE的长;
,求DE的长;
(3)连接EF,求证:EF是⊙O的切线.
【答案】(1) 见解析; (2)3![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)根据圆周角定理得到∠BAC=90°,根据三角形的内角和得到∠ACB=60°根据切线的性质得到∠OAF=90°,∠DBC=90°,于是得到∠D=∠AFC=30°由相似三角形的判定定理即可得到结论;
(2)根据S△AOC=![]() ,得到S△ACF=
,得到S△ACF=![]() ,通过△ACF∽△DAE,求得S△DAE=
,通过△ACF∽△DAE,求得S△DAE=![]() ,过A作AH⊥DE于H,解直角三角形得到AH=
,过A作AH⊥DE于H,解直角三角形得到AH=![]() DH=
DH=![]() DE,由三角形的面积公式列方程即可得到结论;
DE,由三角形的面积公式列方程即可得到结论;
(3)根据全等三角形的性质得到OE=OF,根据等腰三角形的性质得到∠OFG=![]() (180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
(180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
试题解析:(1)证明:∵BC是⊙O的直径,∴∠BAC=90°,∵∠ABC=30°,∴∠ACB=60°
∵OA=OC,∴∠AOC=60°,∵AF是⊙O的切线,∴∠OAF=90°,∴∠AFC=30°,∵DE是⊙O的切线,∴∠DBC=90°,∴∠D=∠AFC=30,∵∠DAE=ACF=120°,∴△ACF∽△DAE;
(2)∵∠ACO=∠AFC+∠CAF=30°+∠CAF=60°,∴∠CAF=30°,∴∠CAF=∠AFC,∴AC=CF,∴OC=CF,∵S△AOC=![]() ,∴S△ACF=
,∴S△ACF=![]() ,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=
,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=![]() BD,∴AF=
BD,∴AF=![]() BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴
BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴![]() ,∵△ACF∽△DAE,∴
,∵△ACF∽△DAE,∴![]() =
=![]() ,∴S△DAE=
,∴S△DAE=![]() ,过A作AH⊥DE于H,∴AH=
,过A作AH⊥DE于H,∴AH=![]() DH=
DH=![]() DE,∴S△ADE=
DE,∴S△ADE=![]() DEAH=
DEAH=![]() ×
×![]()
![]() =
=![]() ,∴DE=
,∴DE=![]() ;
;
(3)∵∠EOF=∠AOB=120°,∴∠OEB=∠AFO,在△AOF与△BOE中,∵∠OBE=∠OAF,∠OEB=∠AFO,OA=OB,∴△AOF≌△BEO,∴OE=OF,∴∠OFG=![]() (180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
(180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
【题型】解答题
【结束】
25
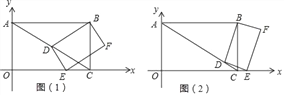
【题目】如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2![]() ,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
(1)填空:点B的坐标为 ;
(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;
(3)①求证:![]() ;
;
②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
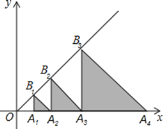
【题目】如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA2=1,则OA2015的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扫黑除恶”受到广大人民的关注,某中学对部分学生就“扫黑除恶”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“很了解”部分所对应扇形的圆心角为_______;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com