
【题目】如图,抛物线y=-![]() x2-
x2-![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-
与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-![]() ).
).
(1)求直线AC的解析式;
(2)如图1,P为直线AC上方抛物线上的一动点,当△PBD的面积最大时,过P作PQ⊥x轴于点Q,M为抛物线对称轴上的一动点,过M作y轴的垂线,垂足为点N,连接PM、NQ,求PM+MN+NQ的最小值;
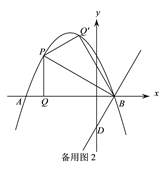
(3)在(2)问的条件下,将得到的△PBQ沿PB翻折得到△PBQ′,将△PBQ′沿直线BD平移,记平移中的△PBQ′为△P′B′Q″,在平移过程中,设直线P′B′与x轴交于点E,则是否存在这样的点E,使得△B′EQ″为等腰三角形?若存在,求此时OE的长.
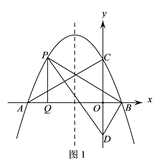

【答案】(1)直线AC的表达式为![]() ;(2)
;(2)![]() 的最小值为
的最小值为![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】分析:(1)求出![]() 两点坐标,利用待定系数法即可解决问题;
两点坐标,利用待定系数法即可解决问题;
![]() 过点P作y轴的平行线交直线BD于点F, 设点
过点P作y轴的平行线交直线BD于点F, 设点![]()
![]() ,则
,则![]() ,表示出
,表示出![]() 的长度,根据
的长度,根据![]() ,构建出二次函数,根据二次函数的性质求出最值即可.
,构建出二次函数,根据二次函数的性质求出最值即可.
![]() 分三种情况进行讨论即可.
分三种情况进行讨论即可.
详解:(1)![]()
![]() 、
、![]() 、
、![]()
设直线AC的表达式为![]() ,将
,将![]() 、
、![]() 代入解析式:
代入解析式:
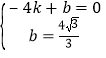 可得
可得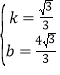 则直线AC的表达式为
则直线AC的表达式为![]() ;
;
(2)可得直线BD的解析式为![]() ,过点P作y轴的平行线交直线BD于点F,
,过点P作y轴的平行线交直线BD于点F,
设点![]()
![]() ,则
,则![]() .
.
![]() ,
,
![]() .
.
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 最大;
最大;
则![]() ,过点P作对称轴
,过点P作对称轴![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,可得
,可得![]()
作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,交
,交![]() 轴与点
轴与点![]() ,
,
再过点![]() 作对称轴
作对称轴![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,即
,即![]() 、
、![]() 为所求点.
为所求点.
此时![]()
![]() ,则最小值为
,则最小值为![]() ;
;
(3)当![]() 时,
时,![]() 或
或![]()
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别是AD,BC边上的点,且AE=CF.
(1)求证:四边形BFDE是平行四边形;
(2)若AB=12,AE=5,cos∠BFE=![]() ,求矩形ABCD的周长.
,求矩形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级为奖励参加校运动会的运动员,分别用160元和120元购买了相同数量的甲、乙两种奖品,其中每件甲种奖品比每件乙种奖品贵4元.
请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
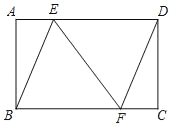
【题目】如图,等边△AOB的边长为4,点P从点O出发,沿OA以每秒1个单位的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.在点P从O向A运动的过程中,当△PCA为直角三角形时t的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
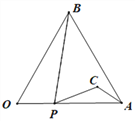
【题目】如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度![]() ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为![]() ,在山坡的坡顶D处测得铁架顶端A的仰角为
,在山坡的坡顶D处测得铁架顶端A的仰角为![]() ,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
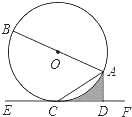
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
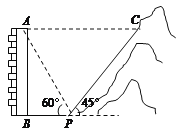
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30 m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
(1)求居民楼AB的高度;
(2)求C、A之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
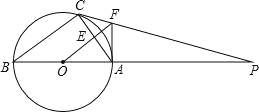
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC,交AC于点E,交PC于点F,连接AF.
(1)求证:AF是⊙O的切线;
(2)已知⊙O的半径为4,AF=3,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家将一种电视机按进价提高35%后定价,然后打出“九折酬宾,外送50元出租车费”的广告,结果每台电视机获利208元.
(1)求每台电视机的进价;
(2)另有一家商家出售同类产品,按进价提高40%,然后打出“八折酬宾”的广告,如果你想买这种产品,应选择哪一个商家?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com