
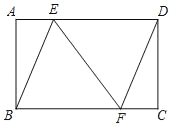
【题目】如图,在矩形ABCD中,点E,F分别是AD,BC边上的点,且AE=CF.
(1)求证:四边形BFDE是平行四边形;
(2)若AB=12,AE=5,cos∠BFE=![]() ,求矩形ABCD的周长.
,求矩形ABCD的周长.
【答案】(1)证明见解析(2)62
【解析】分析:(1)先求出![]() ,然后根据一组对边平行且相等的四边形是平行四边形证明四边形
,然后根据一组对边平行且相等的四边形是平行四边形证明四边形![]() 为平行四边形;
为平行四边形;
(2)由三角函数和勾股定理求出![]() ,得出
,得出![]() ,即可得出答案.
,即可得出答案.
详解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC.AB=CD,
∵AE=CF,
∴DE=BF.
∴四边形BFDE是平行四边形。
(2)∵矩形ABCD,
∴![]()
过点E作EG⊥BC于G.
∵![]()
∴四边形ABGE是矩形,
∴AE=BG=5,AB=EG=12.
∵在Rt△EFG中,![]()
∴![]()
设FG=3x,EF=5x,
∴![]()
∴x=3.
∴FG=3x=9,
∴BC=BG+FG+CF=5+9+5=19.
∴矩形ABCD的周长=19×2+12×2=62.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上,且
上,且![]() ,
,![]() .下列四个判断中,不正确的是( )
.下列四个判断中,不正确的是( )
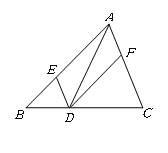
A. 四边形![]() 是平行四边形
是平行四边形
B. 如果![]() ,那么四边形
,那么四边形![]() 是矩形
是矩形
C. 如果![]() 平分平分∠BAC,那么四边形 AEDF 是菱形
平分平分∠BAC,那么四边形 AEDF 是菱形
D. 如果AD⊥BC 且 AB=AC,那么四边形 AEDF 是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
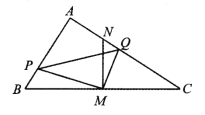
【题目】在△ABC 中,∠BAC=90°,AB<AC,M 是 BC 边的中点,MN⊥BC交 AC 于点 N,动点 P 在线段 BA 上以每秒![]() cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
(1)△PBM 与△QNM 相似吗?请说明理由;
(2)若∠ABC=60°,AB=4 ![]() cm.
cm.
①求动点 Q 的运动速度;
②设△APQ 的面积为 s(cm2),求 S 与 t 的函数关系式.(不必写出 t 的取值范围)
(3)探求 BP、PQ、CQ 三者之间的数量关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[知识背景]:
数轴上,点A,B表示的数为a,b,则A,B两点的距离AB=|a﹣b|,A、B的中点P表示的数为![]() .
.
[知识运用]:
已知式子(a+4)x3+2x2﹣x+3是关于x的二次三项式,且二次项系数为b,且a,b在数轴上对应的点分别为A,B(如图1),解答下列问题:
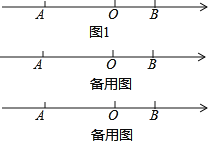
(1)a= ,b= ,AB= ;
(2)若点A以每秒2个单位的长度沿数轴向右运动,t秒后到达原点O,求t的值;
(3)若点A,B都以每秒2个单位长度的速度沿数轴向右运动到达点M和点N,而O点不动,经过t秒后,M,O,N三点中,其中一点是另外两点的中点,求此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种空调共40台.已知购进一台甲种空调比购进一台乙种空调进价多0.2万元;用36万元购进乙种空调数量是用18万元购进甲种空调数量的4倍.请解答下列问题:
(1)求甲、乙两种空调每台进价各是多少万元?
(2)若商场预计投入资金不多于11.5万元用于购买甲、乙两种空调,且购进甲种空调至少14台,商场有哪几种购进方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
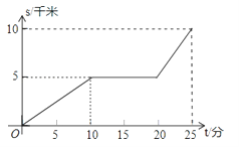
【题目】某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
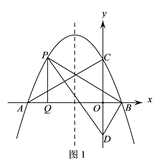
【题目】如图,抛物线y=-![]() x2-
x2-![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-
与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-![]() ).
).
(1)求直线AC的解析式;
(2)如图1,P为直线AC上方抛物线上的一动点,当△PBD的面积最大时,过P作PQ⊥x轴于点Q,M为抛物线对称轴上的一动点,过M作y轴的垂线,垂足为点N,连接PM、NQ,求PM+MN+NQ的最小值;
(3)在(2)问的条件下,将得到的△PBQ沿PB翻折得到△PBQ′,将△PBQ′沿直线BD平移,记平移中的△PBQ′为△P′B′Q″,在平移过程中,设直线P′B′与x轴交于点E,则是否存在这样的点E,使得△B′EQ″为等腰三角形?若存在,求此时OE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com