
����Ŀ��ij�̳������ס������ֿյ���40̨����֪����һ̨���ֿյ��ȹ���һ̨���ֿյ����۶�0.2��Ԫ����36��Ԫ�������ֿյ���������18��Ԫ�������ֿյ�������4���������������⣺
��1����ס������ֿյ�ÿ̨���۸��Ƕ�����Ԫ��
��2�����̳�Ԥ��Ͷ���ʽ���11.5��Ԫ���ڹ���ס������ֿյ����ҹ������ֿյ�����14̨���̳����ļ��ֹ���������
���𰸡���1���յ�ÿ̨�Ľ���Ϊ0.4��Ԫ�����ҿյ�ÿ̨�Ľ���Ϊ0.2��Ԫ����2���̳��������ֹ������������������ֿյ�14̨�����ֿյ�26̨�����������ֿյ�15̨�����ֿյ�25̨�����������ֿյ�16̨�����ֿյ�24̨�����������ֿյ�17̨�����ֿյ�23̨��
��������
��1����յ�ÿ̨�Ľ���Ϊx��Ԫ�����ҿյ�ÿ̨�Ľ���Ϊ��x��0.2����Ԫ����������36��Ԫ�������ֿյ���������18��Ԫ�������ֿյ�������4�����г����̣���֮�ɵã�
��2���蹺�����ֿյ�m̨�������ֿյ���40��m��̨������Ͷ���ʽ���11.5��Ԫ���г�����m�IJ���ʽ����֮���m��ȡֵ��Χ���̶��õ�����m�Ŀ���ȡֵ���Ӷ��ɵ����з�����
�⣺��1����յ�ÿ̨�Ľ���Ϊx��Ԫ�����ҿյ�ÿ̨�Ľ���Ϊ��x��0.2����Ԫ��
�������⣬�ã�![]() ��
��
��ã�x��0.4��
�����飺x��0.4��ԭ��ʽ���̵Ľ⣬
���Լյ�ÿ̨�Ľ���Ϊ0.4��Ԫ�����ҿյ�ÿ̨�Ľ���Ϊ0.2��Ԫ��
��2���蹺�����ֿյ�m̨�������ֿյ���40��m��̨��
�������⣬�ã�0.4m+0.2��40��m����11.5��
��ã�m��17.5��
��m��14��
��14��m��17.5��
������m��ֵ������14��15��16��17��
�����̳��������ֹ���������
�ٹ������ֿյ�14̨�����ֿյ�26̨��
�ڹ������ֿյ�15̨�����ֿյ�25̨��
�۹������ֿյ�16̨�����ֿյ�24̨��
�ܹ������ֿյ�17̨�����ֿյ�23̨��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����A��2��0����ֱ��l��y�ύ�ڵ�B��tan��OAB= ![]() ��ֱ��l�ϵĵ�Pλ��y����࣬�ҵ�y��ľ���Ϊ1��
��ֱ��l�ϵĵ�Pλ��y����࣬�ҵ�y��ľ���Ϊ1��
��1����ֱ��l�ı���ʽ��
��2��������������y= ![]() ��ͼ����P����m��ֵ��
��ͼ����P����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�������˿ͣ������һ�ִ����:��һ�����������������4����ͬ��С�����Ϸֱ���С�0Ԫ����"10Ԫ������20Ԫ������30Ԫ��������.�涨:�˿��ڱ�����һ����������200Ԫ���Ϳ������������Ⱥ���������С��(ÿһ�������Ż�).ij�˿պ�����200Ԫ����ù˿�����ù���ȯ�Ľ�����30Ԫ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����AD�С�O�ڵ�A����C�� ![]() ���е㣬�����н��ۣ���OC��AE����EC��BC���ۡ�DAE����ABE����AC��OE��������ȷ����( )
���е㣬�����н��ۣ���OC��AE����EC��BC���ۡ�DAE����ABE����AC��OE��������ȷ����( )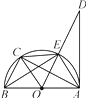
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ���е�A(1��0)����A��һ����������A1(��1��1)���ڶ��ε�A1��������A2(2��1)�������ε�A2����A3(��2��2)�����Ĵε�A3������������A4(3��2)���������˹���������ȥ�����A2 019���A2 020֮��ľ�����( )
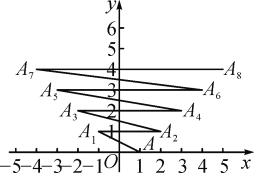
A.2021B.2020C.2019D.2 018
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AM��BN����A=60������P������AM��һ���㣨���A���غϣ���BC��BD�ֱ�ƽ�֡�ABP�͡�PBN���ֱ�����AM�ڵ�C��D��
��1�����CBD�Ķ�����
��2������P�˶�ʱ����APB���ADB֮���������ϵ�Ƿ���֮�����仯�������仯����д������֮��Ĺ�ϵ����˵�����ɣ����仯����д���仯���ɣ�
��3������P�˶���ʹ��ACB=��ABDʱ��ֱ��д����ABC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���36��Ԫ����A��B������Ʒ�����������6��Ԫ������ۺ��ۼ����±���
A | B | |
����(Ԫ/��) | 1200 | 1000 |
�ۼ�(Ԫ/��) | 1380 | 1200 |
��ע���������ۼۣ����ۣ�
(1) ���̳�����A��B������Ʒ�����ټ�?
(2) �̳��ڶ�����ԭ���۹���A��B������Ʒ������B����Ʒ�ļ������䣬������A����Ʒ�ļ����ǵ�һ�ε�2����A����Ʒ��ԭ�۳��ۣ���B����Ʒ�������ۣ���������Ʒ������ϣ�Ҫʹ�ڶ��ξ�Ӫ�����������81600Ԫ��B����Ʒ����ۼ�Ϊÿ������Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC���ܳ�Ϊ30cm����D��E���ڱ�BC�ϣ���ABC��ƽ���ߴ�ֱ��AE������ΪQ����ACB��ƽ���ߴ�ֱ��AD������ΪP����BC=11cm����DE�ij�Ϊ____cm��
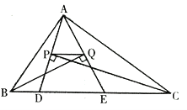
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ܻ���(x��1)(x99��x98��x97������x��1�����������������⣬���ǿ�����˼��һ�£��Ӽ��������֣�Ȼ����ɳ�һЩ������
��1���ֱ����и�ʽ��
��(x��1)(x��1����___________��
��(x��1)(x2��x��1����___________��
��(x��1)(x3��x2��1����___________��
����
�ɴ����ǿ��Եõ���(x��1��(x99��x98��x97������x��1����________________��
��2��������������Ľ��ۼ��㣺
299��298��297������2��1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com