
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是 ![]() 的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )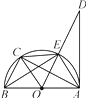
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】由C为 ![]() 的中点,利用垂径定理的逆定理得出OC⊥BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE⊥BE,即可确定出OC∥AE,故A正确;
的中点,利用垂径定理的逆定理得出OC⊥BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE⊥BE,即可确定出OC∥AE,故A正确;
由C为 ![]() 的中点,即
的中点,即 ![]() ,利用等弧对等弦,得到BC=EC,故B正确;
,利用等弧对等弦,得到BC=EC,故B正确;
由AD为圆的切线,得到AD⊥OA,进而确定出一对角互余,再由直角三角形ABE中两锐角互余,利用同角的余角相等,得到∠DAE=∠ABE,故C正确;
AC不一定垂直于OE,故D错误.
故答案为:D
利用垂径定理的逆定理得出OC⊥BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE⊥BE,即可确定出OC∥AE;利用等弧对等弦,得到BC=EC;利用同角的余角相等,得到∠DAE=∠ABE.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】若x满足(x-4) (x-9)=6,求(x-4)2+(x-9)2的值.
解:设x-4=a,x-9=b,则(x-4)(x-9)=ab=6,a-b=(x-4)-(x-9)=5,
∴(x-4)2+(x-9)2=a2+b2=(a-b)2+2ab=52+2×6=37
请仿照上面的方法求解下面问题:
(1)若x满足(x-2)(x-5)=10,求(x-2)2 + (x-5)2的值
(2)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF作正方形,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AD,CB=CE.
(1)当∠ABC=90°时(如图①),∠EBD= °;
(2)当∠ABC=n°(n≠90)时(如图②),求∠EBD 的度数(用含 n 的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次向右跳动至A1(-1,1),第二次向左跳动至A2(2,1),第三次向右跳动至A3(-2,2),第四次向左跳动至A4(3,2)依照此规律跳动下去,点A第2020次跳动至A2020的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字,并完成证明;
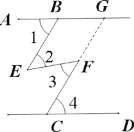
已知:如图,∠1=∠4,∠2=∠3,求证:AB∥CD;
证明:如图,延长CF交AB于点G
∵∠2=∠3
∴BE∥CF( )
∴∠1= ( )
又∠1=∠4
∴∠4= ( )
∴AB∥CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某移动通信公司推出了如下两种移动电话计费方式,
月使用费/元 | 主叫限定时间/分钟 | 主叫超时费(元/分钟) | |
方式一 | 30 | 600 | 0.20 |
方式二 | 50 | 600 | 0.25 |
说明:月使用费固定收取,主叫不超过限定时间不再收费,超过部分加收超时费.例如,方式一每月固定交费30元,当主叫计时不超过300分钟不再额外收费,超过300分钟时,超过部分每分钟加收0.20元(不足1分钟按1分钟计算)
(1)请根据题意完成如表的填空;
月主叫时间500分钟 | 月主叫时间800分钟 | |
方式一收费/元 |
| 130 |
方式二收费/元 | 50 |
|
(2)设某月主叫时间为t(分钟),方式一、方式二两种计费方式的费用分别为y1(元),y2(元),分别写出两种计费方式中主叫时间t(分钟)与费用为y1(元),y2(元)的函数关系式;
(3)请计算说明选择哪种计费方式更省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种空调共40台.已知购进一台甲种空调比购进一台乙种空调进价多0.2万元;用36万元购进乙种空调数量是用18万元购进甲种空调数量的4倍.请解答下列问题:
(1)求甲、乙两种空调每台进价各是多少万元?
(2)若商场预计投入资金不多于11.5万元用于购买甲、乙两种空调,且购进甲种空调至少14台,商场有哪几种购进方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,1),B(3,1),C(3,﹣1),D(1,﹣1)构成正方形ABCD,以AB为边做等边△ABE,则∠ADE和点E的坐标分别为( )

A. 15°和(2,1+![]() )
)
B. 75°和(2,![]() ﹣1)
﹣1)
C. 15°和(2,1+![]() )或75°和(2,
)或75°和(2,![]() ﹣1)
﹣1)
D. 15°和(2,1+![]() )或75°和(2,1﹣
)或75°和(2,1﹣![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com