
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
【答案】
(1)解:由题意可得:(1)y=(x-50)[50+5(100-x)]
=(x-50)(-5x+550)
=-5x2+800x-27500
∴ ![]() 与
与 ![]() 之间的函数关系为:
之间的函数关系为: ![]() .
.
(2)解:y=-5x2+800x-27500
=-5(x-80)2+4500
∵a=-5<0,
∴抛物线开口向下.
∵50≤ ![]() ≤100,对称轴是直线
≤100,对称轴是直线 ![]() =80,
=80,
∴当 ![]() =80时,
=80时, ![]() 最大=4500.
最大=4500.
(3)解:当 ![]() =4000时,-5(
=4000时,-5( ![]() -80)2+4500=4000,解得
-80)2+4500=4000,解得 ![]() =70,
=70, ![]() =90,
=90,
又∵ ![]() 的图象开口向下,
的图象开口向下,
∴当70≤ ![]() ≤90时,每天的销售利润不低于4000元.
≤90时,每天的销售利润不低于4000元.
由每天的总成本不超过7000元,得50(-5 ![]() +550)≤7000,解得
+550)≤7000,解得 ![]() ≥82,
≥82,
∴82≤ ![]() ≤90,
≤90,
∵50≤ ![]() ≤100,
≤100,
∴销售单价应该控制在82元至90元(包括端点)之间.
【解析】(1)根据每天的销售利润y=每一件的利润![]() 每天的销售量,即可求出函数解析式。
每天的销售量,即可求出函数解析式。
(2)求出(1)中函数的顶点坐标,即可求出结论。
(3)先求出y=4000时对应的自变量x的值,结合二次函数的性质,得出每天的销售利润不低于4000元时自变量的取值范围;再根据每天的总成本≤7000,建立不等式求解,即可求出销售单价应控制的范围。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: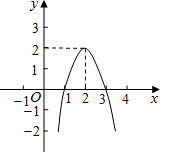
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c<0的解集;
(3)若方程ax2+bx+c+k=0有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试根据图中信息,解答下列问题.
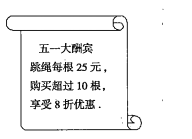
(1)一次性购买6根跳绳需_____元,一次性购买12根跳绳需______元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
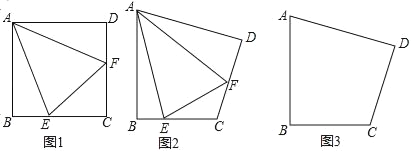
【题目】已知在四边形ABCD中,点E、F分别是BC、CD边上的一点.
(1)如图1:当四边形ABCD是正方形时,且∠EAF=45°,则EF、BE、DF满足的数量关系是 ,请说明理由;
(2)如图2:当AB=AD,∠B=∠D=90°,∠EAF是∠BAD的一半,问:(1)中的数量关系是否还存在? (填是或否)
(3)在(2)的条件下,将点E平移到BC的延长线上,请在图3中补全图形,并写出EF、BE、DF的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
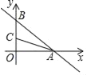
【题目】在平面直角坐标系中,已知一次函数y=﹣![]() x+6与x,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )
A. (0,3) B. (0,![]() ) C. (0,
) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a<0)的对称轴为x=1,交x轴的一个交点为(x1 , 0),且﹣1<x1<0,有下列5个结论:①abc>0;②9a﹣3b+c<0;③2c<3b;④(a+c)2<b2;⑤a+b>m(am+b)(m≠1的实数)其中正确的结论有( )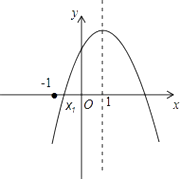
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
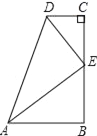
【题目】在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com