
【题目】试根据图中信息,解答下列问题.
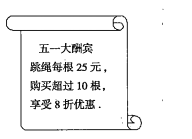
(1)一次性购买6根跳绳需_____元,一次性购买12根跳绳需______元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
【答案】(1)150;240;(2)11根.
【解析】
(1)根据单价×数量=总价,求出6根跳绳需多少元;购买12根跳绳,超过10根,打八折是指现价是原价的80%,用单价×数量×0.8即可求出购买12根跳绳需多少元;
(2)有这种可能,可以设小红购买x跳绳根,那么小明购买x-2根跳绳,列出方程25x×0.8=25(x-2)-5,解答即可.
解:(1)一次性购买6根跳绳需25×6=150(元);
一次性购买12根跳绳需25×12×0.8=240(元);
故答案为:150;240.
(2)设小红购买x跳绳根,那么小明购买(x-2)根跳绳,
25x×0.8=25(x-2)-5,
解得:x=11;
小明购买了:11-2=9根.
答:小红购买11根跳绳.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D、E分别是BC.AD的中点,AF∥BC交CE的延长线于F.则四边形AFBD的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F. 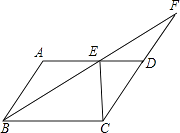
(1)若∠F=20°,求∠A的度数;
(2)若AB=5,BC=8,CE⊥AD,求ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县“贡江新区”位于贡江南岸,由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贯江北岸的老城区相呼应,构建成“一江两岸”的城市新格局。为建设市民河堤漫步体闲通道,贯江新区现有一段长为180米的河堤整治任务由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天。
(1)根据题意,甲、乙两名同学分别列出的方程如下
甲:![]()
乙:![]()
根据甲、乙两名同学所列的方程请你分别指出以下代数式表示的意义:
甲:![]() 表示______________,
表示______________,![]() 表示__________________;
表示__________________;
乙:![]() 表示______________,
表示______________,![]() 表示__________________.
表示__________________.
(2)请你从甲、乙两名同学的解答思路中选择你事欢的一种思路,求A、B两个工程队分别整治河堤的长度,需写出完整的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
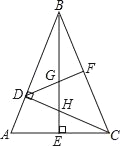
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D、E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)求证:BH=AC;
(2)求证:BG2﹣GE2=EA2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,![]() 求证
求证![]()
(2)如图,![]() 为垂足,
为垂足,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .求
.求![]() 的度数.
的度数.
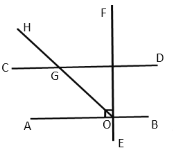
(3)已知![]()
①如图1,求![]() 的度数;
的度数;
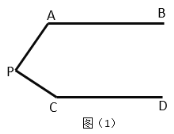
②如图2,![]() 和
和![]() 的平分线
的平分线![]() 相交于点
相交于点![]() ,求
,求![]() 的度数;
的度数;
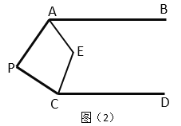
③在图2中,画![]() 和
和![]() 平分线相交于点
平分线相交于点![]() ,求
,求![]() 的度数(直接写出结果即可)
的度数(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简求值:(2+a)(2-a)+a(a-2b)+3a5b÷(-a2b)4,其中ab=-![]() .
.
(2)因式分解:a(n-1)2-2a(n-1)+a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com