
【题目】如图,![]() ,
,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则下列结论正确是______(填序号)①
,则下列结论正确是______(填序号)①![]() ②
②![]() 是
是![]() 的平分线 ③
的平分线 ③![]() 是等腰三角形 ④
是等腰三角形 ④![]() 的周长
的周长![]() .
.
【答案】①②③④
【解析】
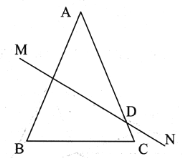
由△ABC中,∠A=36°,AB=AC,根据等腰三角形的性质与三角形内角和定理,即可求得∠C的度数;又由线段垂直平分线的性质,易证得△ABD是等腰三角形,继而可求得∠ABD与∠DBC的度数,证得BD是∠ABC的平分线,然后由∠DBC=36°,∠C=72°,证得∠BDC=72°,易证得△DBC是等腰三角形,个等量代换即可证得④△BCD的周长=AB+BC.
∵△ABC中,∠A=36°,AB=AC,
∴∠ABC=∠C=![]() =72°,
=72°,
故①正确;
∵DM是AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A=36°,
∴∠DBC=∠ABC-∠ABD=36°,
∴∠ABD=∠DBC,
∴BD是∠ABC的平分线;
故②正确;
∵∠DBC=36°,∠C=72°,
∴∠BDC=180°-36°-72°=72°,
∴∠BDC=∠C,
∴BC=BD,
∴△DBC是等腰三角形;
故③正确;
∵BD=AD,
∴△BCD的周长=BD+BC+CD=AC+BC=AB+BC,
故④正确;
故答案为:①②③④.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
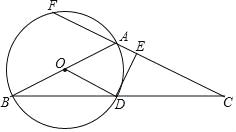
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE⊥AC;
(2)若DE+EA=8,⊙O的半径为10,求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:
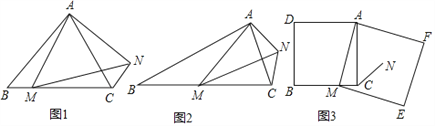
如图1,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为__________;
(2)深入探究:
如图2,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
(3)拓展延伸:
如图3,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN=![]() ,试求EF的长.
,试求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
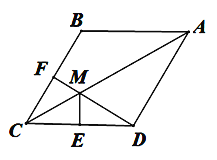
【题目】(本题满分10分)如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E, ∠BAC=∠CDF.
(1)求证BC=2CE;
(2)求证AM=DF+ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
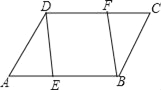
【题目】如图,已知E、F分别是平行四边形ABCD的边AB、CD上的两点,且∠CBF=∠ADE.(1)求证:△ADE≌△CBF;
(2)判定四边形DEBF是否是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣![]() x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题中选择一个,七年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)将上面的条形统计图补充完整;
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少度?
(3)如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
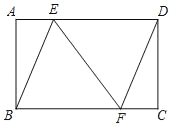
【题目】如图,在矩形ABCD中,点E,F分别是AD,BC边上的点,且AE=CF.
(1)求证:四边形BFDE是平行四边形;
(2)若AB=12,AE=5,cos∠BFE=![]() ,求矩形ABCD的周长.
,求矩形ABCD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com