
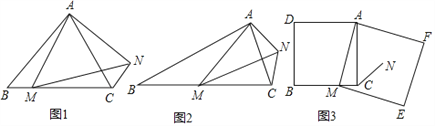
【题目】(1)问题发现:
如图1,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为__________;
(2)深入探究:
如图2,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
(3)拓展延伸:
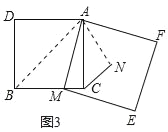
如图3,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN=![]() ,试求EF的长.
,试求EF的长.
【答案】(1)NC∥AB(2)∠ABC=∠ACN,理由见解析;(3)EF= ![]() .
.
【解析】分析:(1)根据△ABC,△AMN为等边三角形,得到AB=AC,AM=AN且∠BAC=∠MAN=60°从而得到∠BAC-∠CAM=∠MAN-∠CAM,即∠BAM=∠CAN,证明△BAM≌△CAN,即可得到BM=CN.
(2)根据△ABC,△AMN为等腰三角形,得到AB:BC=1:1且∠ABC=∠AMN,根据相似三角形的性质得到![]() ,利用等腰三角形的性质得到∠BAC=∠MAN,根据相似三角形的性质即可得到结论;
,利用等腰三角形的性质得到∠BAC=∠MAN,根据相似三角形的性质即可得到结论;
(3)如图3,连接AB,AN,根据正方形的性质得到∠ABC=∠BAC=45°,∠MAN=45°,根据相似三角形的性质得出![]() ,得到BM=2,CM=8,再根据勾股定理即可得到答案.
,得到BM=2,CM=8,再根据勾股定理即可得到答案.
详解:(1)NC∥AB,理由如下:
∵△ABC与△MN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
在△ABM与△ACN中,
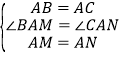 ,
,
∴△ABM≌△ACN(SAS),
∴∠B=∠ACN=60°,
∵∠ANC+∠ACN+∠CAN=∠ANC+60°+∠CAN=180°,
∴∠ANC+∠MAN+∠BAM=∠ANC+60°+∠CAN=∠BAN+∠ANC=180°,
∴CN∥AB;
(2)∠ABC=∠ACN,理由如下:
∵![]() =1且∠ABC=∠AMN,
=1且∠ABC=∠AMN,
∴△ABC~△AMN
∴![]() ,
,
∵AB=BC,
∴∠BAC=![]() (180°﹣∠ABC),
(180°﹣∠ABC),
∵AM=MN
∴∠MAN=![]() (180°﹣∠AMN),
(180°﹣∠AMN),
∵∠ABC=∠AMN,
∴∠BAC=∠MAN,
∴∠BAM=∠CAN,
∴△ABM~△ACN,
∴∠ABC=∠ACN;
(3)如图3,连接AB,AN,
∵四边形ADBC,AMEF为正方形,
∴∠ABC=∠BAC=45°,∠MAN=45°,
∴∠BAC﹣∠MAC=∠MAN﹣∠MAC
即∠BAM=∠CAN,
∵![]() ,
,
∴![]() ,
,
∴△ABM~△ACN
∴![]() ,
,
∴![]() =cos45°=
=cos45°=![]() ,
,
∴![]() ,
,
∴BM=2,
∴CM=BC﹣BM=8,
在Rt△AMC,
AM=![]() ,
,
∴EF=AM=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知O是直线AB上一点,∠AOC=45°36’,OD平分∠BOC,求∠AOD的度数.完成下列推理过程:
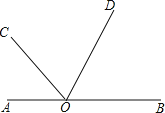
解:由题意可知,∠AOB是平角,
∠AOB= +∠BOC
因为∠AOC=45°36′
所以∠BOC= ° ′
又因为OD平分∠BOC
∴∠COD=![]() ∠BOC= ° ′
∠BOC= ° ′
∴∠AOD=∠ +∠ = ° ′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地。两车同时出发,匀速行驶。图2是客车、货车离C站的路程y![]() ,y
,y![]() (千米)与行驶时间x(小时)之间的函数关系图象。
(千米)与行驶时间x(小时)之间的函数关系图象。
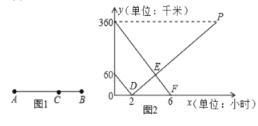
(1)填空:A,B两地相距___千米;货车的速度是___千米/时。
(2)求两小时后,货车离C站的路程y![]() 与行驶时间x之间的函数表达式;
与行驶时间x之间的函数表达式;
(3)客、货两车何时距离不大于30km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为a、宽为b的长方形纸片上,剪掉一个大圆和两个半径相等的小圆.
(1)列出剩余纸片(图中阴影部分)面积的代数式;(结果要求化简)
(2)当a=6cm,b=4cm时,求阴影部分的面积,(π取3.14)
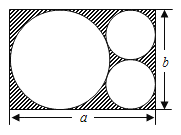
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD=BF,∠ACD=90°,AE平分∠BAC,BF⊥AE,交AC的延长线于F,且垂足为E,则下列结论:①AD=2BF; ②BF=AF;③AC+CD=AB;④AB=BF;⑤AD=2BE.其中正确的结论有( )
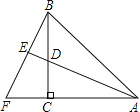
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,边OA的长度为8,对角线AC=10,抛物线y=![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式并求出S最大时的m值;
②在S最大的情况下,在抛物线y=![]() x2+bx+c的对称轴上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
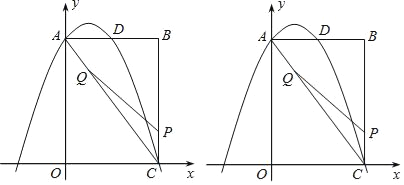
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并填空
(1)探究:平面上有n个点(n>2)且任意3个点不在同一条直线上,经过每两个点画一条直线,一共能画多少条直线? 根据基本事实,我们知道两点确定一条直线,平面上有2个点时,可以画![]() 条直线,平面内有3个不在同一直线上点时,可画
条直线,平面内有3个不在同一直线上点时,可画![]() 条直线,那么平面上有4个不在同一直线上的点时,可以画 条, 平面上有5个不在同一直线上的点时,可以画 条,以此类推,平面上有n个不在同一直线上的点时,可以画 条
条直线,那么平面上有4个不在同一直线上的点时,可以画 条, 平面上有5个不在同一直线上的点时,可以画 条,以此类推,平面上有n个不在同一直线上的点时,可以画 条
(2)运用:某足球比赛中有10个球队进行单循环比赛(每两队之间必须比赛一场),一共进行多少场比赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上,且
上,且![]() ,
,![]() .下列四个判断中,不正确的是( )
.下列四个判断中,不正确的是( )
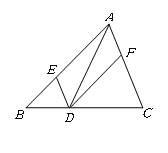
A. 四边形![]() 是平行四边形
是平行四边形
B. 如果![]() ,那么四边形
,那么四边形![]() 是矩形
是矩形
C. 如果![]() 平分平分∠BAC,那么四边形 AEDF 是菱形
平分平分∠BAC,那么四边形 AEDF 是菱形
D. 如果AD⊥BC 且 AB=AC,那么四边形 AEDF 是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com