
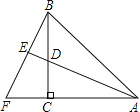
【题目】如图,AD=BF,∠ACD=90°,AE平分∠BAC,BF⊥AE,交AC的延长线于F,且垂足为E,则下列结论:①AD=2BF; ②BF=AF;③AC+CD=AB;④AB=BF;⑤AD=2BE.其中正确的结论有( )
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
根据∠ACB=90°,BF⊥AE,得出∠ACB=∠BED=∠BCF=90°,推出∠F=∠ADC,证△BCF≌△ACD,根据全等三角形的性质即可判断①②;假如AC+CD=AB,求出∠F+∠FBC=90°,即可判断③④,证根据全等三角形的判定ASA得出△BEA≌△FEA,推出BE=EF,即可判断⑤.
∵∠ACB=90°,BF⊥AE,
∴∠ACB=∠BED=∠BCF=90°,
∴∠F+∠FBC=90°,∠BDE+∠FBC=90°,
∴∠F=∠BDE,
∵∠BDE=∠ADC,
∴∠F=∠ADC,
∵AC=BC,
∴△BCF≌△ACD,
∴AD=BF,∴①错误;
∵AF>AD,
∴BF≠AF②错误;
∵△BCF≌△ACD,
∴CD=CF,
∴AC+CD=AF,
∵△BCF≌△ACD,
∴CD=CF,
∴AC+CD=AF,
又∵AB=AF,
∴AC+CD=AB.
∴③正确;
∵BF=AC,AC<AF=AB,
∴AB>BF,
∴④错误;
由△BCF≌△ACD,
∴AD=BF,
∵AE平分∠BAF,AE⊥BF,
∴∠BEA=∠FEA=90°,∠BAE=∠FAE,
∵AE=AE,∴△BEA≌△FEA,
∴BE=EF,
∴⑤正确;
故选B


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某制笔企业欲将200件产品运往![]() ,
,![]() ,
,![]() 三地销售,要求运往
三地销售,要求运往![]() 地的件数是运往
地的件数是运往![]() 地件数的2倍,各地的运费如图所示.设安排
地件数的2倍,各地的运费如图所示.设安排![]() 件产品运往
件产品运往![]() 地.
地.
|
|
| |
产品件数(件) |
|
| |
运费(元) |
|
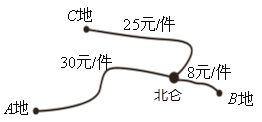
(1)①根据信息补全上表空格.②若设总运费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式及自变量的取值范围.
的函数关系式及自变量的取值范围.
(2)若运往![]() 地的产品数量不超过运往
地的产品数量不超过运往![]() 地的数量,应怎样安排
地的数量,应怎样安排![]() ,
,![]() ,
,![]() 三地的运送数量才能达到运费最少.
三地的运送数量才能达到运费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网格是由边长为1的小正方形组成,点A,B,C位置如图所示,若点![]() ,
,![]() .
.

(1)建立适当的平面直角坐标系,并写出点C坐标(______,______);点B到x轴的距离是______,点C到y轴的距离是______;
(2)在平面直角坐标系中找一点D,使A,B,C,D为顶点的四边形的所有内角都相等,再画出四边形ABCD.
(3)请你说出线段AB经过怎样的变换得到线段DC的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
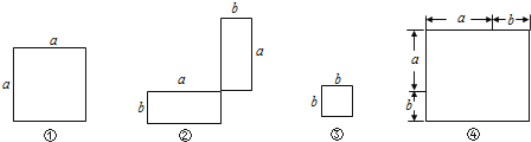
① ; ② ; ③ ; ④ .
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示: ;
(3)利用(2)的结论计算992+2×99×1+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB+BC=BE,则∠B的度数是( )
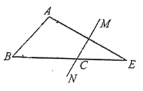
A. 45°B. 60°C. 50°D. 25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:
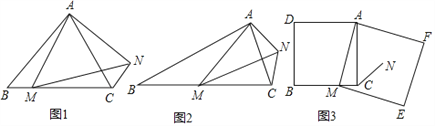
如图1,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为__________;
(2)深入探究:
如图2,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
(3)拓展延伸:
如图3,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN=![]() ,试求EF的长.
,试求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
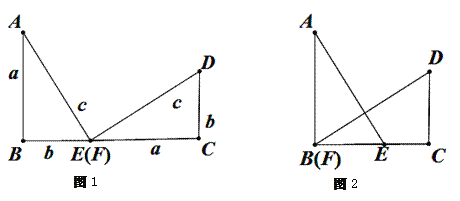
【题目】(1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE ≌△FCD,AE![]() DF,请你证明:
DF,请你证明:![]() ;
;
(2)在(1)中,固定△FCD,再将△ABE沿着BC平移到如图2的位置(此时B,F重合),请你重新证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
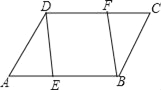
【题目】如图,已知E、F分别是平行四边形ABCD的边AB、CD上的两点,且∠CBF=∠ADE.(1)求证:△ADE≌△CBF;
(2)判定四边形DEBF是否是平行四边形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com