【题目】如图，在△ABE中，∠A=105°，AE的垂直平分线MN交BE于点C,且AB+BC=BE,则∠B的度数是（ ）
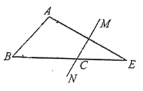
A. 45°B. 60°C. 50°D. 25°
【答案】C
【解析】
首先连接AC，由AE的垂直平分线MN交BE于点C，可得AC=EC，又由AB+BC=BE，易证得AB=AC，然后由等腰三角形的性质与三角形内角和定理，求得∠BAE=∠BAC+∠CAE=180°-4∠E+∠E=105°，继而求得答案．
连接AC，
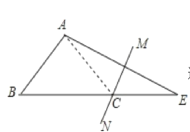
∵MN是AE的垂直平分线，
∴AC=EC，
∴∠CAE=∠E，
∵AB+BC=BE，BC+EC=BE，
∴AB=EC=AC，
∴∠B=∠ACB，
∵∠ACB=∠CAE+∠E=2∠E，
∴∠B=2∠E，
∴∠BAC=180°∠B∠ACB=180°4∠E，
∵∠BAE=∠BAC+∠CAE=180°4∠E+∠E=105°
解得：∠E=25°，
∴∠B=2∠E=50°.
故选：C.
科目：初中数学 来源： 题型：
【题目】公园门票价格规定如下：
某校七年级（1）（2）两个班共104人去游园，其中（1）班有40多人，且不足50人，经估算，如果两个班都以班为单位进行购票，则一共应付1240元，问：
（1）两个班各有多少个学生？
（2）如果两班联合起来，作为一个团体票能省多少钱？如果七（1）班单独组织去游园，作为组织者的你如何购票才最省钱？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使ABCD为正方形（如图），现有下列四种选法，你认为其中错误的是（ ）
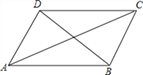
A. ①② B. ②③ C. ①③ D. ②④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图各图是棱长为1cm的小正方体摆成的，如图①中,从正面看有1个正方形，表面积为6cm2；如图②中,从正面看有3个正方形，表面积为18cm2；如图③，从正面看有6个正方形，表面积为36cm2；…
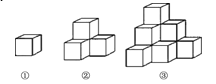
(1)第6个图中，从正面看有多少个正方形?表面积是多少?
(2)第n个图形中，从正面看有多少个正方形?表面积是多少?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）23﹣17﹣（﹣7）+（﹣16）
（2）
（3）﹣22÷（﹣4）3+|0.8﹣1|×（2
）2
（4）4xy+（3y2﹣2x2）﹣（5xy﹣2x2）﹣4y2
（5）先化简，再求值：x﹣2（x﹣y2）+（﹣
x+
y2），其中x＝﹣
，y＝3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD=BF，∠ACD=90°，AE平分∠BAC，BF⊥AE，交AC的延长线于F，且垂足为E，则下列结论：①AD=2BF; ②BF=AF;③AC+CD=AB;④AB=BF;⑤AD=2BE.其中正确的结论有（ ）
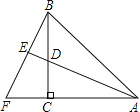
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC 中，∠BAC＝90°，AB＝AC，D 是 AC 边上一动点， CE⊥BD 于 E．
(1)如图（1），若 BD 平分∠ABC 时，①求∠ECD 的度数；②求证：BD＝2EC；
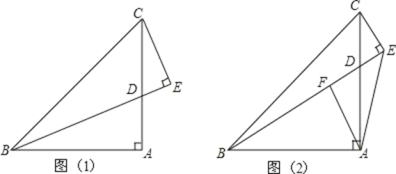
(2)如图（2），过点 A 作 AF⊥BE 于点 F，猜想线段 BE，CE，AF 之间的数量关系并证明你的猜想．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数轴上两个质点A.B所对应的数为8、4，A.B两点各自以一定的速度在数轴上运动，且A点的运动速度为2个单位/秒。
（1）点A.B两点同时出发相向而行，在4秒后相遇，求B点的运动速度；
（2）A、B两点以(1)中的速度同时出发，向数轴正方向运动，几秒钟时两者相距6个单位长度；
（3）A、B两点以(1)中的速度同时出发，向数轴负方向运动，与此同时，C点从原点出发作同方向的运动，且在运动过程中，始终有CA=2CB，若干秒钟后，C停留在10处，求此时B点的位置?
查看答案和解析>>
科目：初中数学 来源： 题型：
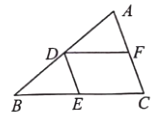
【题目】如图，在△ABC中，D、E、F分别为边AB、BC、CA的中点．
（1）求证：四边形DECF是平行四边形．
（2）当AC、BC满足何条件时，四边形DECF为菱形？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com