
【题目】某制笔企业欲将200件产品运往![]() ,
,![]() ,
,![]() 三地销售,要求运往
三地销售,要求运往![]() 地的件数是运往
地的件数是运往![]() 地件数的2倍,各地的运费如图所示.设安排
地件数的2倍,各地的运费如图所示.设安排![]() 件产品运往
件产品运往![]() 地.
地.
|
|
| |
产品件数(件) |
|
| |
运费(元) |
|
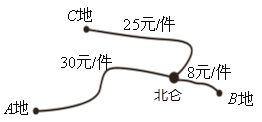
(1)①根据信息补全上表空格.②若设总运费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式及自变量的取值范围.
的函数关系式及自变量的取值范围.
(2)若运往![]() 地的产品数量不超过运往
地的产品数量不超过运往![]() 地的数量,应怎样安排
地的数量,应怎样安排![]() ,
,![]() ,
,![]() 三地的运送数量才能达到运费最少.
三地的运送数量才能达到运费最少.
【答案】(1)①见解析;②![]() ,
,![]() ;(2)安排运往
;(2)安排运往![]() ,
,![]() ,
,![]() 三地的产品件数分别为40件、80件,80件时,运费最少.
三地的产品件数分别为40件、80件,80件时,运费最少.
【解析】
(1)①根据运往B地的产品件数=总件数-运往A地的产品件数-运往B地的产品件数;运费=相应件数×一件产品的运费,即可补全图表;
②根据题意列出函数解析式即可;
(2)根据运往B地的件数不多于运往C地的件数,列出不等式,利用一次函数的性质解答即可;
解:(1)①根据信息填表
|
|
| |
产品件数(件) |
| ||
运费(元) |
|
|
②由题意列式![]() (
(![]() 且
且![]() 是整数)(取值范围1分,没写
是整数)(取值范围1分,没写![]() 是整数不扣分)
是整数不扣分)
(2)若运往![]() 地的产品数量不超过运往
地的产品数量不超过运往![]() 地的数量则:
地的数量则:![]() ,解得
,解得![]() ,
,
由![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而增大,
的增大而增大,
∴当![]() 时,
时,![]() 最小,
最小,![]() .
.
此时![]() ,
,![]() .
.
所以安排运往![]() ,
,![]() ,
,![]() 三地的产品件数分别为40件、80件,80件时,运费最少.
三地的产品件数分别为40件、80件,80件时,运费最少.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第二次将点A向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离不小于20,那么n的最小值是( )
![]()
A. 12B. 13C. 14D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
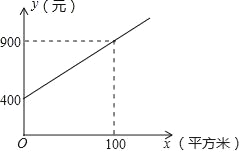
【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园门票价格规定如下:

某校七年级(1)(2)两个班共104人去游园,其中(1)班有40多人,且不足50人,经估算,如果两个班都以班为单位进行购票,则一共应付1240元,问:
(1)两个班各有多少个学生?
(2)如果两班联合起来,作为一个团体票能省多少钱?如果七(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O是直线AB上一点,∠AOC=45°36’,OD平分∠BOC,求∠AOD的度数.完成下列推理过程:
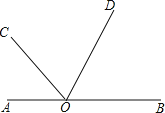
解:由题意可知,∠AOB是平角,
∠AOB= +∠BOC
因为∠AOC=45°36′
所以∠BOC= ° ′
又因为OD平分∠BOC
∴∠COD=![]() ∠BOC= ° ′
∠BOC= ° ′
∴∠AOD=∠ +∠ = ° ′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用院墙的一段再围三面篱笆,形成一个矩形花园![]() (院墙
(院墙![]() 长
长![]() 米),现有
米),现有![]() 米长的篱笆.
米长的篱笆.

(1)请你设计一种围法(篱笆必须用完),使矩形花园的面积为![]() 米.
米.
(2)如何设计可以使得围成的矩形面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,延长线段AB至C使BC=2AB,延长线段BA至D使AD=3AB,点E是线段DB的中点,点F是线段AC的中点,若EF=10cm,求AB、CD的长度

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD=BF,∠ACD=90°,AE平分∠BAC,BF⊥AE,交AC的延长线于F,且垂足为E,则下列结论:①AD=2BF; ②BF=AF;③AC+CD=AB;④AB=BF;⑤AD=2BE.其中正确的结论有( )
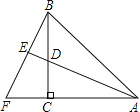
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com