
【题目】如图,某中学准备在校园里利用院墙的一段再围三面篱笆,形成一个矩形花园![]() (院墙
(院墙![]() 长
长![]() 米),现有
米),现有![]() 米长的篱笆.
米长的篱笆.

(1)请你设计一种围法(篱笆必须用完),使矩形花园的面积为![]() 米.
米.
(2)如何设计可以使得围成的矩形面积最大?最大面积是多少?
【答案】见详解.
【解析】
(1)设AB为xm,则BC为(40-2x)m,根据题意可得等量关系:矩形的面积=长×宽=150,根据等量关系列出方程,再解即可;
(2)根据题意和图形可以得到S与x之间的函数关系,将函数关系式化为顶点式,即可解答本题.
解:(1)设AB为xm,则BC为(40-2x)m,根据题意可得:
X(40-2x)=150
解得:x1=![]() ,x2=15.
,x2=15.
:当x=![]() 时,40-2x=30>25.故不满足题意,应舍去.
时,40-2x=30>25.故不满足题意,应舍去.
②当x=15时,40-2x=10<25,故当x=15时,满足实际要求.
∴当x=15 时,使矩形花园的面积为![]() 米.
米.
(2)设矩形的面积为S,则依意得:
S= X(40-2x)=-2x2+40x=-2(x-5)2+50
∴当x=5,时S有最大值.最大值为50.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的,该市电费收费标准如下表(按月结算):
每月用电量度 | 电价/(元/度) |
不超过150度的部分 | 0.50元/度 |
超过150度且不超过250度的部分 | 0.65元/度 |
超过250度的部分 | 0.80元/度 |
问:(1)某居民12月份用电量为180度,请问该居民12月应缴交电费多少元?
(2)设某月的用电量为![]() 度(
度(![]() ),试写出不同电量区间应缴交的电费.
),试写出不同电量区间应缴交的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段达到节水的目的,如表是调控后的价目表.
价目表
每月用水量 | 单价 |
不超过6吨的部分 | 2元/吨 |
超出6吨不超出10吨的部分 | 4元/吨 |
超出10吨的部分 | 8元/吨 |
注:水费按月结算.
(1)若该户居民8月份用水8吨,则该用户8月应交水费 元;若该户居民9月份应交水费26元,则该用户9月份用水量为 吨;
(2)若该户居民10月份应交水费30元,求该用户10月份用水量;
(3)若该户居民11月、12月共用水18吨,共交水费52元,求11月、12月各应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
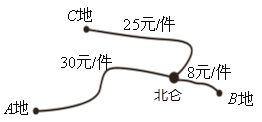
【题目】某制笔企业欲将200件产品运往![]() ,
,![]() ,
,![]() 三地销售,要求运往
三地销售,要求运往![]() 地的件数是运往
地的件数是运往![]() 地件数的2倍,各地的运费如图所示.设安排
地件数的2倍,各地的运费如图所示.设安排![]() 件产品运往
件产品运往![]() 地.
地.
|
|
| |
产品件数(件) |
|
| |
运费(元) |
|
(1)①根据信息补全上表空格.②若设总运费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式及自变量的取值范围.
的函数关系式及自变量的取值范围.
(2)若运往![]() 地的产品数量不超过运往
地的产品数量不超过运往![]() 地的数量,应怎样安排
地的数量,应怎样安排![]() ,
,![]() ,
,![]() 三地的运送数量才能达到运费最少.
三地的运送数量才能达到运费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
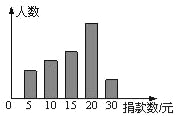
【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐20元的人数为24人,
(1)他们一共抽查了多少人?捐款数不少于20元的概率是多少?
(2)这组数据的众数是 (元)、中位数是 (元);
(3)若该校共有660名学生,请估算全校学生共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上点A表示的数为6,B是数轴上在左侧的一点,且A,B两点间的距离为10。动点P从点A出发,以每秒6个单位长度的度沿数轴向左匀速运动,设运动时间为t![]() 秒。
秒。
![]()
(1)数轴上点B表示的数是______;当点P运动到AB的中点时,它所表示的数是_____。
(2)动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,求:
①当点P运动多少秒时,点P追上点Q?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网格是由边长为1的小正方形组成,点A,B,C位置如图所示,若点![]() ,
,![]() .
.

(1)建立适当的平面直角坐标系,并写出点C坐标(______,______);点B到x轴的距离是______,点C到y轴的距离是______;
(2)在平面直角坐标系中找一点D,使A,B,C,D为顶点的四边形的所有内角都相等,再画出四边形ABCD.
(3)请你说出线段AB经过怎样的变换得到线段DC的?
查看答案和解析>>
科目:初中数学 来源: 题型:
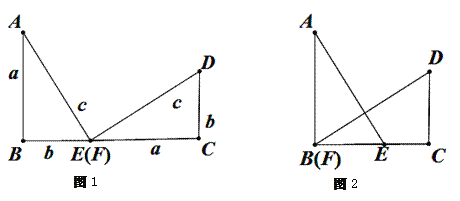
【题目】(1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE ≌△FCD,AE![]() DF,请你证明:
DF,请你证明:![]() ;
;
(2)在(1)中,固定△FCD,再将△ABE沿着BC平移到如图2的位置(此时B,F重合),请你重新证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com