
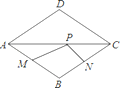
【题目】如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则![]() 的最小值是( )
的最小值是( )
A. 2B. ![]() C. 1D.
C. 1D. ![]()
【答案】C
【解析】
首先作点M关于AC的对称点M′,连接M′N交AC于P,此时MP+NP有最小值.然后证明四边形PMBN为菱形,即可求出MP+NP=BM+BN=BC=1.
作点M关于AC的对称点M′,连接M′N交AC于P,此时MP+NP有最小值

∵菱形ABCD关于AC对称,M是AB边上的中点,
∴M′是AD的中点,
又N是BC边上的中点,
∴AM′∥BN,AM′=BN,
∴四边形AM′BN是平行四边形,
∴PN∥AB,
又N是BC边上的中点,
∴PN是△CAB的中位线,
∴P是AC中点,
∴PM∥BN,PM=BN,
∴四边形PMBN是平行四边形,
∵BM=BN,
∴平行四边形PMBN是菱形。
∴MP+NP=BM+BN=BC=1.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】公园门票价格规定如下:

某校七年级(1)(2)两个班共104人去游园,其中(1)班有40多人,且不足50人,经估算,如果两个班都以班为单位进行购票,则一共应付1240元,问:
(1)两个班各有多少个学生?
(2)如果两班联合起来,作为一个团体票能省多少钱?如果七(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用院墙的一段再围三面篱笆,形成一个矩形花园![]() (院墙
(院墙![]() 长
长![]() 米),现有
米),现有![]() 米长的篱笆.
米长的篱笆.

(1)请你设计一种围法(篱笆必须用完),使矩形花园的面积为![]() 米.
米.
(2)如何设计可以使得围成的矩形面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
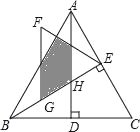
【题目】如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4![]() ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为_____.
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,延长线段AB至C使BC=2AB,延长线段BA至D使AD=3AB,点E是线段DB的中点,点F是线段AC的中点,若EF=10cm,求AB、CD的长度

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
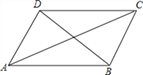
A. ①② B. ②③ C. ①③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图各图是棱长为1cm的小正方体摆成的,如图①中,从正面看有1个正方形,表面积为6cm2;如图②中,从正面看有3个正方形,表面积为18cm2;如图③,从正面看有6个正方形,表面积为36cm2;…
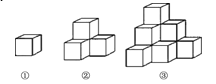
(1)第6个图中,从正面看有多少个正方形?表面积是多少?
(2)第n个图形中,从正面看有多少个正方形?表面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两个质点A.B所对应的数为8、4,A.B两点各自以一定的速度在数轴上运动,且A点的运动速度为2个单位/秒。
![]()
(1)点A.B两点同时出发相向而行,在4秒后相遇,求B点的运动速度;
(2)A、B两点以(1)中的速度同时出发,向数轴正方向运动,几秒钟时两者相距6个单位长度;
(3)A、B两点以(1)中的速度同时出发,向数轴负方向运动,与此同时,C点从原点出发作同方向的运动,且在运动过程中,始终有CA=2CB,若干秒钟后,C停留在10处,求此时B点的位置?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com