
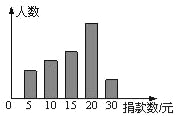
【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐20元的人数为24人,
(1)他们一共抽查了多少人?捐款数不少于20元的概率是多少?
(2)这组数据的众数是 (元)、中位数是 (元);
(3)若该校共有660名学生,请估算全校学生共捐款多少元?
【答案】(1)![]() (2)20,15;(3)10500
(2)20,15;(3)10500
【解析】分析:(1)根据捐15元和20元得人数共39人及这两组所占的总人数比例可求出总人数,
(2)众数是一组数据中出现次数最多的数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;
(3)求出这组数据的平均数,再估算.
详解:(1)设捐15元的人数为5x,则根据题意捐20元的人数为8x.
∴5x+8x=39,
∴x=3,
∴一共调查了3x+4x+5x+8x+2x=66(人),
可得:捐款30元的人数为:6人,捐款20元的人数为:24人,
则捐款数不少于20元的概率是: ![]() ;
;
(2)5个组的人数分别为9,12,15,24,6.
所以这组数据的众数是20(元),中位数是15(元).
故答案为:20,15;
(3)全校学生共捐款:(9×5+12×10+15×15+24×20+6×30)÷66×660=10500(元).


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为1,点P是射线AD的上的一个动点,点A关于直线BP的对称点是点Q,设AP=x.
(1)求当D,Q,B三点在同一直线上时对应的x的值.
(2)当△CDQ为等腰三角形时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动公司推出一款话费套餐活动,资费标准见下表
套餐月费/元 | 套餐内容 | 套餐外资费 | |
主叫限定时间/分钟 | 被叫 | 主叫超时费(元/分钟) | |
58 | 50 | 免费 | 0.25 |
88 | 150 | 0.20 | |
118 | 350 | 0.15 | |
说明:①主叫:主动打电话给别人;被叫:接听别人打进来的电话. ②若办理的是月使用费为58元的套餐,主叫时间不超过50分钟时,当月话费即为58元;主叫时间为60分钟,则当月话费为 | |||
小文办理的是月使用费为88元的套餐,亮亮办理的是月使用费为118元的套餐.
(1)①小文当月的主叫时间为220分钟,则该月她的话费为__________元.
②亮亮当月的主叫时间为220分钟,则该月他的话费为____________元.
(2)某月小文与亮亮的主叫时间都为m分钟(![]() ),请用含m的代数式表示该月他们的话费差.
),请用含m的代数式表示该月他们的话费差.
(3)11月小文和亮亮的话费相同,但主叫时间比亮亮少100分钟,则小文的主叫时间是_______分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园门票价格规定如下:

某校七年级(1)(2)两个班共104人去游园,其中(1)班有40多人,且不足50人,经估算,如果两个班都以班为单位进行购票,则一共应付1240元,问:
(1)两个班各有多少个学生?
(2)如果两班联合起来,作为一个团体票能省多少钱?如果七(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
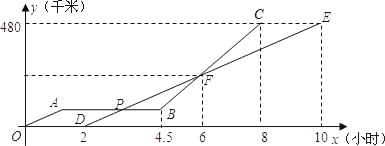
【题目】甲、乙两辆汽车沿同一路线赶赴距出发地480km的目的地,乙车比甲车晚出发2h(从甲车出发时开始计时).图中折线OABC、线段DE分别表示甲、乙两车所行路程y(km)与时间x(h)之间的函数关系对应的图象(线段AB表示甲车出发不足2h因故障停车检修).请根据图象所提供的信息,解决以下问题:
(1)求乙车所行路程y与时间x之间的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇.(写出解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用院墙的一段再围三面篱笆,形成一个矩形花园![]() (院墙
(院墙![]() 长
长![]() 米),现有
米),现有![]() 米长的篱笆.
米长的篱笆.

(1)请你设计一种围法(篱笆必须用完),使矩形花园的面积为![]() 米.
米.
(2)如何设计可以使得围成的矩形面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
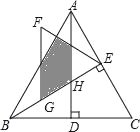
【题目】如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4![]() ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为_____.
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
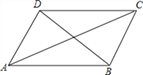
A. ①② B. ②③ C. ①③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,D 是 AC 边上一动点, CE⊥BD 于 E.
(1)如图(1),若 BD 平分∠ABC 时,①求∠ECD 的度数;②求证:BD=2EC;
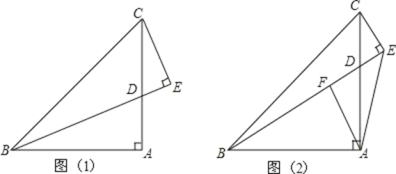
(2)如图(2),过点 A 作 AF⊥BE 于点 F,猜想线段 BE,CE,AF 之间的数量关系并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com