
【题目】如图,已知正方形ABCD边长为1,点P是射线AD的上的一个动点,点A关于直线BP的对称点是点Q,设AP=x.
(1)求当D,Q,B三点在同一直线上时对应的x的值.
(2)当△CDQ为等腰三角形时,求x的值.

【答案】(1)![]() ;(2)
;(2)![]() ,
, ![]() ,
, ![]() .
.
【解析】分析: (1)求x,通常都是考虑勾股定理,选择直角三角形PDE,发现PE,DE,PD都可用x来表示,进而易得方程,求解即可.
(2)若△CDQ为等腰三角形,则边CD比为改等腰三角形的一腰或者底边.又Q点为A点关于PB的对称点,则AB=QB,以点B为圆心,以AB的长为半径画弧,则Q点只能在弧AB上.若CD为腰,以点C为圆心,以CD的长为半径画弧,两弧交点即为使得△CDQ为等腰三角形(CD为腰)的Q点.若CD为底边,则作CD的垂直平分线,其与弧AC的交点即为使得△CDQ为等腰三角形(CD为底)的Q点.则如图所示共有三个Q点,那么也共有3个P点.作辅助线,利用直角三角形性质求之即可.
详解:
(1)连接DB,若Q点落在BD上,由AP=x,则PD=1﹣x,PQ=x.
∵∠PDQ=45°,
∴PD=![]() PQ,
PQ,
即1﹣x=![]() x,
x,
∴x=![]() ﹣1,
﹣1,
(2)①如图1,连接BQ1、CQ1,作PQ1⊥BQ1交AD于P,过点Q1,作EF⊥AD于E,交BC于F.
∵△BCQ1为等边三角形,正方形ABCD边长为1,
∴Q1F=![]() Q1E=
Q1E=![]() .
.
在四边形ABPQ1中,
∵∠ABQ1=30°,
∴∠APQ1=150°,
∴△PEQ1为含30°的直角三角形,
∴PE=![]() Q1E=
Q1E=![]() .
.
∵AE=![]() ,
,
∴x=AP=AE﹣PE=2﹣![]() .
.
②如图2,连接BQ2,AQ2,过点Q2作PG⊥BQ2,交AD于P,连接BP,过点Q2作EF⊥CD于E,交AB于F.∵EF垂直平分CD,∴EF垂直平分AB,∴AQ2=BQ2.∵AB=BQ2,∴△ABQ2为等边三角形.在四边形ABQP中,∵∠BAD=∠BQP=90°,∠ABQ2=60°,∴∠ABP=30°,
∴x=AP=![]() .
.
③如图4,连接BQ1,CQ1,BQ3,CQ3,过点Q3作BQ3⊥PQ3,交AD的延长线于P,连接BP,过点Q1,作EF⊥AD于E,此时Q3在EF上,不妨记Q3与F重合.
∵△BCQ1为等边三角形,△BCQ3为等边三角形,BC=1,
∴Q1Q2=![]() ,Q1E=
,Q1E=![]() ,
,
∴EF=![]() .
.
在四边形ABQ3P中
∵∠ABF=∠ABC+∠CBQ3=150°,
∴∠EPF=30°,
∴EP=![]() EF=
EF=![]() .
.
∵AE=![]() ,
,
∴x=AP=AE+PE=![]() +2.
+2.

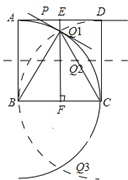
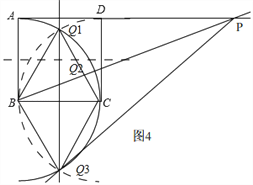
图1 图2
综上所述:△CDQ为等腰三角形时x的值为2﹣![]() ,
, ![]() ,2+
,2+![]() .
.
点睛:本题第一问非常基础,难度较低.第二问因为动点的原因,思路不易找到,这里就需要做题时充分分析已知条件,尤其是新给出的条件.其中求边长是勾股定理的重要应用,是很重要的考点.第三问是一个难度非常高的题目,可以利用尺规作图的思想将满足要求的点Q找全.另外求解各个P点也是考察三角函数及勾股定理的综合应用,有着极高的难度.


科目:初中数学 来源: 题型:
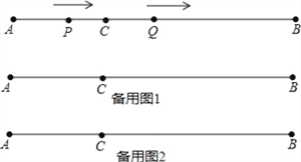
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料并回答问题
观察:有理数-2和-4在数轴上对应的两点之间的距离是![]() ,有理数1和-3在数轴上对应的两点之间的距离是
,有理数1和-3在数轴上对应的两点之间的距离是![]()

归纳:有理数a、b在数轴上对应的两点A.B之间的距离是![]() ,反之,
,反之,![]() 表示有理数a、b在数轴上对应点A.B之间的距离,称之为绝对值的几何意义
表示有理数a、b在数轴上对应点A.B之间的距离,称之为绝对值的几何意义
应用:
(1)如果表示-1的点A和表示x点B之间的距离是2,那么x为________;
(2)方程![]() 的解为________;
的解为________;
(3)小松同学在解方程![]() 时,利用绝对值的几何意义分析得到,该方程的左边表示在数轴上x对应点到1和-2对应点的距离之和,而当
时,利用绝对值的几何意义分析得到,该方程的左边表示在数轴上x对应点到1和-2对应点的距离之和,而当![]() 时,取到它的最小值3,即为1和-2对应的点的距离.由方程右边的值为5可知,满足方程的x对应点在1的右边或-2的左边,若x的对应点在1的右边,利用数轴分析可以看出
时,取到它的最小值3,即为1和-2对应的点的距离.由方程右边的值为5可知,满足方程的x对应点在1的右边或-2的左边,若x的对应点在1的右边,利用数轴分析可以看出![]() ;同理,若x的对应点在-2的左边,可得
;同理,若x的对应点在-2的左边,可得![]() ;故原方程的解是
;故原方程的解是![]() 或
或![]() ;参考小松的解答过程,求方程
;参考小松的解答过程,求方程![]() 的解.
的解.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解食品安全状况,质监部门抽查了甲、乙、丙、丁四个品牌饮料的质量,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题:
(1)这次抽查了四个品牌的饮料共 瓶;
(2)请你在答题卡上补全两幅统计图;
(3)若四个品牌饮料的平均合格率是95%,四个品牌饮料月销售量约20万瓶,请你估计这四个品牌的不合格饮料有多少瓶?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
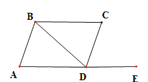
A.∠C=∠CDEB.∠ABD=∠CBDC.∠ABD=∠CDBD.∠C+∠ADC=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的,该市电费收费标准如下表(按月结算):
每月用电量度 | 电价/(元/度) |
不超过150度的部分 | 0.50元/度 |
超过150度且不超过250度的部分 | 0.65元/度 |
超过250度的部分 | 0.80元/度 |
问:(1)某居民12月份用电量为180度,请问该居民12月应缴交电费多少元?
(2)设某月的用电量为![]() 度(
度(![]() ),试写出不同电量区间应缴交的电费.
),试写出不同电量区间应缴交的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,抛物线y=﹣![]() x2﹣
x2﹣![]() x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC
x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC
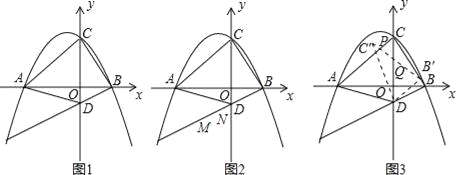
(1)求出直线AD的解析式;
(2)如图2,若在直线AC上方的抛物线上有一点F,当△ADF的面积最大时,有一线段MN=![]() (点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(3)如图3,将△DBC绕点D逆时针旋转α°(0<α°<180°),记旋转中的△DBC为△DB′C′,若直线B′C′与直线AC交于点P,直线B′C′与直线DC交于点Q,当△CPQ是等腰三角形时,求CP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
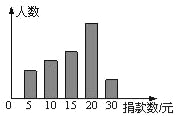
【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐20元的人数为24人,
(1)他们一共抽查了多少人?捐款数不少于20元的概率是多少?
(2)这组数据的众数是 (元)、中位数是 (元);
(3)若该校共有660名学生,请估算全校学生共捐款多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com