
【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的,该市电费收费标准如下表(按月结算):
每月用电量度 | 电价/(元/度) |
不超过150度的部分 | 0.50元/度 |
超过150度且不超过250度的部分 | 0.65元/度 |
超过250度的部分 | 0.80元/度 |
问:(1)某居民12月份用电量为180度,请问该居民12月应缴交电费多少元?
(2)设某月的用电量为![]() 度(
度(![]() ),试写出不同电量区间应缴交的电费.
),试写出不同电量区间应缴交的电费.
【答案】(1)该居民12月份应缴电费94.5元;(2)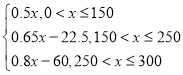
【解析】
(1)根据用电量类型分别进行计算即可;
(2)分三种情况进行讨论,当x不超过150度时,x超过150度,但不超过时250度时和x超过250度时,再分别代入计算即可.
解:(1)由题意,得150×0.50+(180-150)×0.65=94.5(元)
答:该居民12月应缴交电费94.5元;
(2)若某户的用电量为x度,则当x≤150时,应付电费:0.50x元;
当150<x≤250时,应付电费:
0.65(x![]() 150)+75=
150)+75=![]() (元);
(元);
当250<x<300,应付电费:
0.80(x![]() 250)+140=
250)+140=![]() (元).
(元).
∴不同电量区间应缴交的电费为: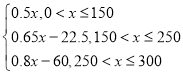 .
.


科目:初中数学 来源: 题型:
【题目】已知点![]() 和直线
和直线![]() (
(![]() 不同时为0),则点
不同时为0),则点![]() 到直线
到直线![]() 的距离
的距离![]() 可用公式
可用公式![]() 计算.
计算.
例如.求点![]() 到直线
到直线![]() 的距离.
的距离.
解:由直线可知![]()
∴![]()
根据以上材料,解答下列问题:
(1) 求点![]() 到直线
到直线![]() 的距离;
的距离;
(2) 求点![]() 到直线
到直线![]() 的距离,并说明点
的距离,并说明点![]() 与直线的位置关系;
与直线的位置关系;
(3)已知直线![]() 与直线
与直线![]() 平行,求两条平行线间的距离.
平行,求两条平行线间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,5), B(a,b),且a,b满足b=![]() +
+![]() -1.
-1.
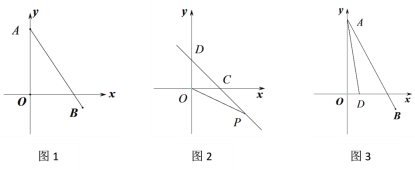
(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第二次将点A向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离不小于20,那么n的最小值是( )
![]()
A. 12B. 13C. 14D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为1,点P是射线AD的上的一个动点,点A关于直线BP的对称点是点Q,设AP=x.
(1)求当D,Q,B三点在同一直线上时对应的x的值.
(2)当△CDQ为等腰三角形时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
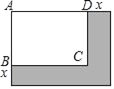
【题目】如图,矩形ABCD的长BC=5,宽AB=3.
(1)若矩形的长与宽同时增加2,则矩形的面积增加 .
(2)若矩形的长与宽同时增加x,此时矩形增加的面积为48,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
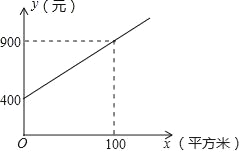
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用院墙的一段再围三面篱笆,形成一个矩形花园![]() (院墙
(院墙![]() 长
长![]() 米),现有
米),现有![]() 米长的篱笆.
米长的篱笆.

(1)请你设计一种围法(篱笆必须用完),使矩形花园的面积为![]() 米.
米.
(2)如何设计可以使得围成的矩形面积最大?最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com