
【题目】已知点![]() 和直线
和直线![]() (
(![]() 不同时为0),则点
不同时为0),则点![]() 到直线
到直线![]() 的距离
的距离![]() 可用公式
可用公式![]() 计算.
计算.
例如.求点![]() 到直线
到直线![]() 的距离.
的距离.
解:由直线可知![]()
∴![]()
根据以上材料,解答下列问题:
(1) 求点![]() 到直线
到直线![]() 的距离;
的距离;
(2) 求点![]() 到直线
到直线![]() 的距离,并说明点
的距离,并说明点![]() 与直线的位置关系;
与直线的位置关系;
(3)已知直线![]() 与直线
与直线![]() 平行,求两条平行线间的距离.
平行,求两条平行线间的距离.
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】工业园区某机械厂的一个车间主要负责生产螺丝和螺母,该车间有工人44人,其中女生人数比男生人数的![]() 倍少
倍少![]() 人,每个工人平均每天可以生产螺丝
人,每个工人平均每天可以生产螺丝![]() 个或者螺母
个或者螺母![]() 个
个
(1)该车间有男生、女生各多少人?
(2)已知一个螺丝与两个螺母配套,为了使每天生产的螺丝螺母恰好配套,应该分配多少工人负责生产螺丝,多少工人负责生产螺母?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张平行四边形纸片ABCD中,画一个菱形,甲、乙两位同学的画法如下:甲:以B,A为圆心,AB长为半径作弧,分别交BC,AD于点E,F,则四边形ABEF为菱形;乙:作∠A,∠B的平分线AE,BF,分别交BC于点E,交AD于点F,则四边形ABEF是菱形;关于甲、乙两人的画法,下列判断正确的是( )
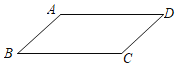
A. 仅甲正确B. 仅乙正确
C. 甲、乙均正确D. 甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
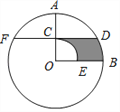
【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.则图中阴影部分的面积为______________.
,交OB于E点.则图中阴影部分的面积为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
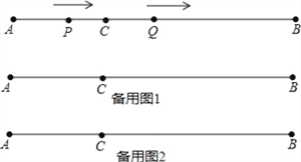
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
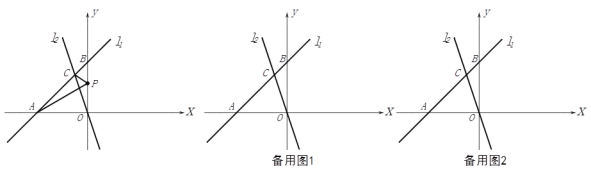
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 轴上一动点.
轴上一动点.
(1)求点![]() 的坐标;
的坐标;
(2)当![]() 的值最小时,求此时
的值最小时,求此时![]() 点的坐标,并求
点的坐标,并求![]() 的最小值;
的最小值;
(3)在平面直角坐标系中是否存在点![]() ,使以点
,使以点![]() 为顶点的四边形是平行四边形,若存在,求出点
为顶点的四边形是平行四边形,若存在,求出点![]() 的坐标;若不存在,请说出理由.
的坐标;若不存在,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
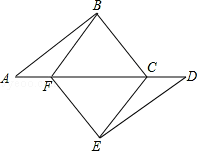
【题目】如图,点A.F、C.D在同一直线上,点B和点E分别在直线AD的两侧,且
AB=DE,∠A=∠D,AF=DC.
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,能判定四边形ABCD为平行四边形的个数是( )
①AB∥CD,AD=BC ; ②AB=CD,AD=BC;③∠A=∠B,∠C=∠D; ④AB=AD,CB=CD.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的,该市电费收费标准如下表(按月结算):
每月用电量度 | 电价/(元/度) |
不超过150度的部分 | 0.50元/度 |
超过150度且不超过250度的部分 | 0.65元/度 |
超过250度的部分 | 0.80元/度 |
问:(1)某居民12月份用电量为180度,请问该居民12月应缴交电费多少元?
(2)设某月的用电量为![]() 度(
度(![]() ),试写出不同电量区间应缴交的电费.
),试写出不同电量区间应缴交的电费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com