
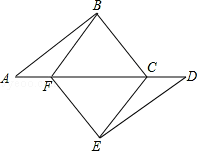
【题目】如图,点A.F、C.D在同一直线上,点B和点E分别在直线AD的两侧,且
AB=DE,∠A=∠D,AF=DC.
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形.
【答案】(1)证明:∵AF=DC,∴AF+FC=DC+FC,即AC=DF。
∵在△ABC和△DEF中,AC=DF,∠A=∠D,AB=DE,
∴△ABC≌DEF(SAS)。∴BC=EF,∠ACB=∠DFE,∴BC∥EF。
∴四边形BCEF是平行四边形.
(2)解:连接BE,交CF与点G,
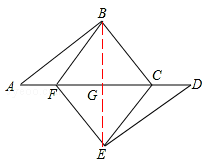
∵四边形BCEF是平行四边形,
∴当BE⊥CF时,四边形BCEF是菱形。
∵∠ABC=90°,AB=4,BC=3,
∴AC=![]() 。
。
∵∠BGC=∠ABC=90°,∠ACB=∠BCG,∴△ABC∽△BGC。
∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
∵FG=CG,∴FC=2CG=![]() ,
,
∴AF=AC﹣FC=5﹣![]() 。
。
∴当AF=![]() 时,四边形BCEF是菱形.
时,四边形BCEF是菱形.
【解析】(1)由AB=DE,∠A=∠D,AF=DC,根据SAS得△ABC≌DEF,即可得BC=EF,且BC∥EF,即可判定四边形BCEF是平行四边形。
(2)由四边形BCEF是平行四边形,可得当BE⊥CF时,四边形BCEF是菱形,所以连接BE,交CF与点G,证得△ABC∽△BGC,由相似三角形的对应边成比例,即可求得AF的值。


科目:初中数学 来源: 题型:
【题目】已知直线l上有一点O,点A,B同时从O出发,在直线l上分别向左,向右作匀速运动,且A,B的速度之比是1:2,设运动时间为ts,
(1)当t=2s时,AB=24cm,此时,
①在直线l上画出A,B两点运动2s时的位置,并回答点A运动的速度是 cm/s,点B的运动速度是 cm/s;
②若点P为直线l上一点,且PA=OP+PB,求![]() 的值;
的值;
(2)在(1)的条件下,若A,B同时按原速度向左运动,再经过几秒,OA=3OB?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
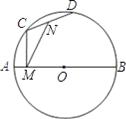
A. 随C、D的运动位置而变化,且最大值为4 B. 随C、D的运动位置而变化,且最小值为2
C. 随C、D的运动位置长度保持不变,等于2 D. 随C、D的运动位置而变化,没有最值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 和直线
和直线![]() (
(![]() 不同时为0),则点
不同时为0),则点![]() 到直线
到直线![]() 的距离
的距离![]() 可用公式
可用公式![]() 计算.
计算.
例如.求点![]() 到直线
到直线![]() 的距离.
的距离.
解:由直线可知![]()
∴![]()
根据以上材料,解答下列问题:
(1) 求点![]() 到直线
到直线![]() 的距离;
的距离;
(2) 求点![]() 到直线
到直线![]() 的距离,并说明点
的距离,并说明点![]() 与直线的位置关系;
与直线的位置关系;
(3)已知直线![]() 与直线
与直线![]() 平行,求两条平行线间的距离.
平行,求两条平行线间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,商洛剧院举行专场音乐会,成人票每张20元,学生票每张5元,为了吸引广大师生来听音乐会,剧院制定了两种优惠方案:
方案一:购买一张成人票赠送一张学生票;
方案二:成人票和学生票都打九折.
我校现有4名老师与若干名(不少于4人)学生听音乐会.
(1)设学生人数为![]() (人),付款总金额为
(人),付款总金额为![]() (元),请分别确定两种优惠方案中
(元),请分别确定两种优惠方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)请你结合参加听音乐会的学生人数,计算说明怎样购票花费少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
![]()
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
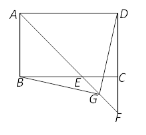
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.
(1)若AB=2,AD=3,求EF的长;
(2)若G是EF的中点,连接BG和DG,求证:DG=BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
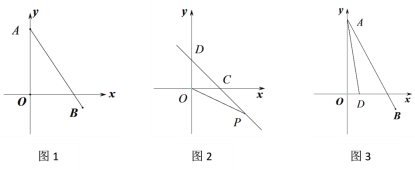
【题目】如图,在平面直角坐标系中,已知A(0,5), B(a,b),且a,b满足b=![]() +
+![]() -1.
-1.
(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com