
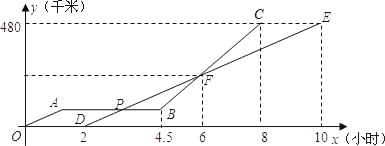
【题目】甲、乙两辆汽车沿同一路线赶赴距出发地480km的目的地,乙车比甲车晚出发2h(从甲车出发时开始计时).图中折线OABC、线段DE分别表示甲、乙两车所行路程y(km)与时间x(h)之间的函数关系对应的图象(线段AB表示甲车出发不足2h因故障停车检修).请根据图象所提供的信息,解决以下问题:
(1)求乙车所行路程y与时间x之间的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇.(写出解题过程)
【答案】(1)y与x的函数关系式为y=60x﹣120;(2)两车在途中第二次相遇时,它们距出发地的路程为240千米;(3)乙车出发3﹣2=1小时,两车在途中第一次相遇
【解析】分析:(1)由图可看出,乙车所行路程y与时间x的成一次函数,使用待定系数法可求得一次函数关系式;
(2)由图可得,交点F表示第二次相遇,F点横坐标为6,代入(1)中的函数即可求得距出发地的路程;
(3)交点P表示第一次相遇,即甲车故障停车检修时相遇,点P的横坐标表示时间,纵坐标表示离出发地的距离,要求时间,则需要把点P的纵坐标先求出;从图中看出,点P的纵坐标与点B的纵坐标相等,而点B在线段BC上,BC对应的函数关系可通过待定系数法求解,点B的横坐标已知,则纵坐标可求.
详解:(1)设乙车所行路程y与时间x的函数关系式为y=k1x+b1,
把(2,0)和(10,480)代入,
得![]() ,解得
,解得![]() ,
,
∴y与x的函数关系式为y=60x-120;
(2)由图可得,交点F表示第二次相遇,
而F点横坐标为6,此时y=60×6-120=240,
∴F点坐标为(6,240),
∴两车在途中第二次相遇时,它们距出发地的路程为240千米;
(3)设线段BC对应的函数关系式为y=k2x+b2,
把(6,240)、(8,480)代入,
得![]() ,
,
解得![]() ,
,
∴y与x的函数关系式为y=120x-480,
∴当x=4.5时,y=120×4.5-480=60.
∴点B的纵坐标为60,
∵AB表示因故停车检修,
∴交点P的纵坐标为60,
把y=60代入y=60x-120中,
有60=60x-120,
解得x=3,
∴交点P的坐标为(3,60),
∵交点P表示第一次相遇,
∴乙车出发3-2=1小时,两车在途中第一次相遇.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
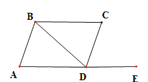
A.∠C=∠CDEB.∠ABD=∠CBDC.∠ABD=∠CDBD.∠C+∠ADC=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上对应的数为x,点B对应的数为y,且点O为数轴上的原点,且![]() .
.
![]()
(1)点A对应的数为______;点B对应的数为______;线段![]() 的长度为_______;
的长度为_______;
(2)若数轴上有一点C,且![]() ,求点C在数轴上对应的数;
,求点C在数轴上对应的数;
(3)若点P从A点出发沿数轴的正方向以每秒2个单位的速度运动,同时Q点从B点出发沿数轴的负方向以每秒4个单位长度的速度运动,运动时间为t秒,当![]() 时,求t的值.
时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D为四家超市,其中超市D距A,B,C三家超市的路程分别为25km,10km,5km.现计划在A,D之间的道路上建一个配货中心P,为避免交通拥堵,配货中心与超市之间的距离不少于2km.假设一辆货车每天从P出发为这四家超市送货各1次,由于货车每次仅能给一家超市送货,因此每次送货后均要返回配货中心P,重新装货后再前往其他超市.设P到A的路程为xkm,这辆货车每天行驶的路程为ykm.
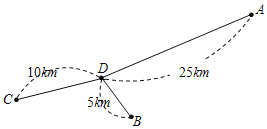
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)直接写出配货中心P建在什么位置,这辆货车每天行驶的路程最短?最短路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
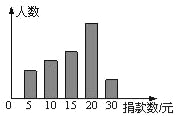
【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐20元的人数为24人,
(1)他们一共抽查了多少人?捐款数不少于20元的概率是多少?
(2)这组数据的众数是 (元)、中位数是 (元);
(3)若该校共有660名学生,请估算全校学生共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com