
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

科目:初中数学 来源: 题型:
【题目】某校在“数学小论文”评比活动中,共征集到论文100篇,对论文评比的分数(分数为整数)整理后,分组画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为l:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有____篇.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,D是BC中点,E是AD中点,过A作AF∥BC

①求证:△AEF≌△DEB;
②求证:四边形ADCF是菱形;
③若AB=5,AC=4,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a、b、c在数轴上的位置如图所示,则:
(1)用“<、>、=”填空:a____0,b____0,c_____0;
(2)用“<、>、=”填空:﹣a____0,a﹣b____0,c﹣a____0;
(3)化简:|﹣a|﹣|a﹣b|+|c﹣a|
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各数填入相应的括号里:
![]() ,5,
,5,![]() ,
,![]() ,0,8,-2,-0.7
,0,8,-2,-0.7![]() ……
……
正数集合{________________________________________…};
负数集合{________________________________________…};
有理数集合{________________________________________…};
无理数集合{________________________________________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 km.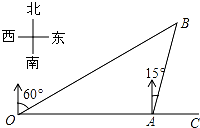
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个可以自由转动的转盘被平均分成4个扇形,分别标有1、2、3、4四个数字,小王和小李各转动一次转盘为一次游戏.当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转). 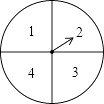
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)求每次游戏结束得到的一组数恰好是方程x2﹣4x+3=0的解的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC、CD. 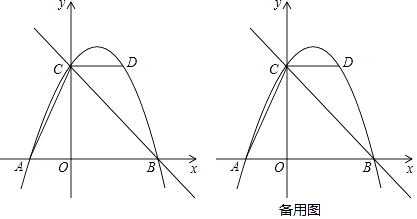
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值,
(1)2x2y﹣[3xy2+2(xy2+2x2y)],其中x=![]() ,y=﹣2.
,y=﹣2.
(2)已知a+b=4,ab=﹣2,求代数式(4a﹣3b﹣2ab)﹣(a﹣6b﹣ab)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com