
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 km.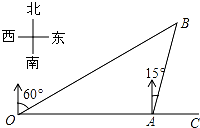
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB两个端点坐标分别为A(a,0),B(0,b),且a,b满足:![]()
(1)填空:a= ,b= .

(2)在坐标轴上是否存在点C,使S△ABC=6,若存在,求出点C的坐标,符不存在,说明理由;
(3)如图2,若将线段Ba平移得到线段OD,其中B点对应O点,A点对应D点,点P(m,n)是线段OD上任意一点,请直接写出m与n的关系式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
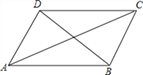
A. ①② B. ②③ C. ①③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两个点A、B所对应的数为a、b,且a、b满足![]() .
.
(1)求AB的长;

(2)若甲、乙分别从A、B两点同时在数轴上相向运动,甲的速度是2个单位/秒,乙的速度比甲的速度快3个单位/秒,求甲乙相遇点所表示的数;

(3)若点C对应的数为—1,在数轴上A点的左侧是否存在一点P,使PA+PB=3PC?若存在,求出点P所对应的数;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并回答问题:
三峡之最
三峡工程是中国,也是世界上最大的水利枢纽工程,是治理和开发长江的关键性骨干工程.它具有防洪、发电、航运等综合效益.
三峡水库总库容![]() 亿立方米,防洪库容
亿立方米,防洪库容![]() 亿立方米,水库调洪可消减洪峰流量达每秒
亿立方米,水库调洪可消减洪峰流量达每秒![]() ─
─![]() 万立方米,是世界上防洪效益最为显著的水利工程.
万立方米,是世界上防洪效益最为显著的水利工程.
三峡水电站总装机![]() 万千瓦,年发电量
万千瓦,年发电量![]() 亿千瓦.时,是世界上最大的电站.
亿千瓦.时,是世界上最大的电站.
三峡水库回水可改善川江![]() 公里的航道,使宜渝船队吨位由现在的
公里的航道,使宜渝船队吨位由现在的![]() 吨级堤高到万吨级,年单向通过能力由
吨级堤高到万吨级,年单向通过能力由![]() 万吨增加到
万吨增加到![]() 万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.
万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.
思考:
![]() 三峡水电站年发电量
三峡水电站年发电量![]() 亿千瓦.时,一个普通家庭一天用电
亿千瓦.时,一个普通家庭一天用电![]() 千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留
千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留![]() 个有效数字)
个有效数字)
![]() 宜都市
宜都市![]() 万人,平均一户
万人,平均一户![]() 个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数).
个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,∠A=36°,AC的垂直平分线MN交AB于D,AC于M,以下结论:
①△BCD是等腰三角形;②射线CD是∠ACB的角平分线;③△BCD的周长C△BCD=AB+BC;④△ADM≌△BCD。
正确的有( )

A. ①② B. ①③ C. ①②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,A(0,4),B(8,0),C(8,4).
⑴ 试说明四边形AOBC是矩形.
⑵ 在x轴上取一点D,将△DCB绕点C逆时针旋转90°得到![]() (点
(点![]() 与点D对应).
与点D对应).
① 若OD=3,求点![]() 的坐标.
的坐标.
② 连接AD'、OD',则AD'+OD'是否存在最小值,若存在,请直接写出最小值及此时点D'的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com