
【题目】为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段达到节水的目的,如表是调控后的价目表.
价目表
每月用水量 | 单价 |
不超过6吨的部分 | 2元/吨 |
超出6吨不超出10吨的部分 | 4元/吨 |
超出10吨的部分 | 8元/吨 |
注:水费按月结算.
(1)若该户居民8月份用水8吨,则该用户8月应交水费 元;若该户居民9月份应交水费26元,则该用户9月份用水量为 吨;
(2)若该户居民10月份应交水费30元,求该用户10月份用水量;
(3)若该户居民11月、12月共用水18吨,共交水费52元,求11月、12月各应交水费多少元?
【答案】(1)20;9.5;(2)该用户10月份用水量为10.25吨;(3)11月份交16元,12月份交36元或11月份交36元,12月份交16元.
【解析】
(1)因为用水量为8 吨,所以计算单价分为两段,列式计算即可;先计算用水量为6吨和10吨的总价,与26对比,发现9月份用水量x的取值范围,从而列出方程求解;
(2)与(1)类似,由题意得出水费30元,用水量超过了10吨,列方程求未知数即可;
(3)设该户居民11月、12月共应交的水费为W元,由题意表示出11月用水量;分三种情况进行讨论:当0≤a≤6时,当6<a≤8时,当8<a<9时,列式表示即可.
解:(1)6×2+(8﹣6)×4=20,
答:该用户8月应交水费20元;
设该用户9月份用水量为x吨,
2×6=12,2×6+(10﹣6)×4=28,
∵12<26<28,
∴6<x<10,
则6×2+4(x﹣6)=26,
x=9.5,
答:该用户9月份用水量为9.5吨;
故答案是:20;9.5;
(2)该用户10月份用水量为y吨,则y>10,
根据题意得:6×2+(10﹣6)×4+8(y﹣10)=30,
y=10.25;
(3)设11月份用水x吨,12月份用水(18﹣x)吨,
①当0≤x≤6时,18﹣x>10,由题意得:2x+2×6+4×4+8[(18﹣x)﹣10]=52.
即:﹣6x+92=52,
解得x=![]() (舍去),
(舍去),
②当6<x≤8时,18﹣x≥10,2×6+4(x﹣6)+2×6+4×4+8[(18﹣x)﹣10]=52,
解得x=7,18﹣x=11.
故11月份的水费是:6×2+1×4=16(元)
12月份的水费是:6×2+4×4+1×8=36(元).
同理可得:11月份交36元,12月份交16元.
答:11月份交16元,12月份交36元或11月份交36元,12月份交16元.


科目:初中数学 来源: 题型:
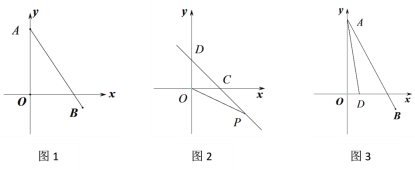
【题目】如图,在平面直角坐标系中,已知A(0,5), B(a,b),且a,b满足b=![]() +
+![]() -1.
-1.
(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
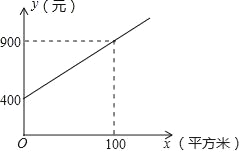
【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动公司推出一款话费套餐活动,资费标准见下表
套餐月费/元 | 套餐内容 | 套餐外资费 | |
主叫限定时间/分钟 | 被叫 | 主叫超时费(元/分钟) | |
58 | 50 | 免费 | 0.25 |
88 | 150 | 0.20 | |
118 | 350 | 0.15 | |
说明:①主叫:主动打电话给别人;被叫:接听别人打进来的电话. ②若办理的是月使用费为58元的套餐,主叫时间不超过50分钟时,当月话费即为58元;主叫时间为60分钟,则当月话费为 | |||
小文办理的是月使用费为88元的套餐,亮亮办理的是月使用费为118元的套餐.
(1)①小文当月的主叫时间为220分钟,则该月她的话费为__________元.
②亮亮当月的主叫时间为220分钟,则该月他的话费为____________元.
(2)某月小文与亮亮的主叫时间都为m分钟(![]() ),请用含m的代数式表示该月他们的话费差.
),请用含m的代数式表示该月他们的话费差.
(3)11月小文和亮亮的话费相同,但主叫时间比亮亮少100分钟,则小文的主叫时间是_______分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园门票价格规定如下:

某校七年级(1)(2)两个班共104人去游园,其中(1)班有40多人,且不足50人,经估算,如果两个班都以班为单位进行购票,则一共应付1240元,问:
(1)两个班各有多少个学生?
(2)如果两班联合起来,作为一个团体票能省多少钱?如果七(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用院墙的一段再围三面篱笆,形成一个矩形花园![]() (院墙
(院墙![]() 长
长![]() 米),现有
米),现有![]() 米长的篱笆.
米长的篱笆.

(1)请你设计一种围法(篱笆必须用完),使矩形花园的面积为![]() 米.
米.
(2)如何设计可以使得围成的矩形面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图各图是棱长为1cm的小正方体摆成的,如图①中,从正面看有1个正方形,表面积为6cm2;如图②中,从正面看有3个正方形,表面积为18cm2;如图③,从正面看有6个正方形,表面积为36cm2;…
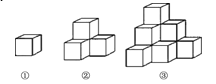
(1)第6个图中,从正面看有多少个正方形?表面积是多少?
(2)第n个图形中,从正面看有多少个正方形?表面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com