
【题目】网格是由边长为1的小正方形组成,点A,B,C位置如图所示,若点![]() ,
,![]() .
.

(1)建立适当的平面直角坐标系,并写出点C坐标(______,______);点B到x轴的距离是______,点C到y轴的距离是______;
(2)在平面直角坐标系中找一点D,使A,B,C,D为顶点的四边形的所有内角都相等,再画出四边形ABCD.
(3)请你说出线段AB经过怎样的变换得到线段DC的?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
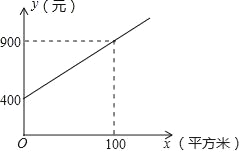
【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用院墙的一段再围三面篱笆,形成一个矩形花园![]() (院墙
(院墙![]() 长
长![]() 米),现有
米),现有![]() 米长的篱笆.
米长的篱笆.

(1)请你设计一种围法(篱笆必须用完),使矩形花园的面积为![]() 米.
米.
(2)如何设计可以使得围成的矩形面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,延长线段AB至C使BC=2AB,延长线段BA至D使AD=3AB,点E是线段DB的中点,点F是线段AC的中点,若EF=10cm,求AB、CD的长度

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
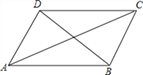
A. ①② B. ②③ C. ①③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地。两车同时出发,匀速行驶。图2是客车、货车离C站的路程y![]() ,y
,y![]() (千米)与行驶时间x(小时)之间的函数关系图象。
(千米)与行驶时间x(小时)之间的函数关系图象。
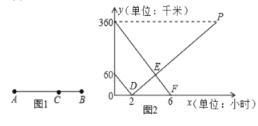
(1)填空:A,B两地相距___千米;货车的速度是___千米/时。
(2)求两小时后,货车离C站的路程y![]() 与行驶时间x之间的函数表达式;
与行驶时间x之间的函数表达式;
(3)客、货两车何时距离不大于30km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图各图是棱长为1cm的小正方体摆成的,如图①中,从正面看有1个正方形,表面积为6cm2;如图②中,从正面看有3个正方形,表面积为18cm2;如图③,从正面看有6个正方形,表面积为36cm2;…
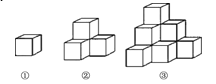
(1)第6个图中,从正面看有多少个正方形?表面积是多少?
(2)第n个图形中,从正面看有多少个正方形?表面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD=BF,∠ACD=90°,AE平分∠BAC,BF⊥AE,交AC的延长线于F,且垂足为E,则下列结论:①AD=2BF; ②BF=AF;③AC+CD=AB;④AB=BF;⑤AD=2BE.其中正确的结论有( )
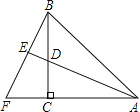
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com