
【题目】如图,已知O是直线AB上一点,∠AOC=45°36’,OD平分∠BOC,求∠AOD的度数.完成下列推理过程:
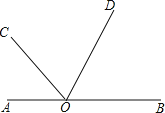
解:由题意可知,∠AOB是平角,
∠AOB= +∠BOC
因为∠AOC=45°36′
所以∠BOC= ° ′
又因为OD平分∠BOC
∴∠COD=![]() ∠BOC= ° ′
∠BOC= ° ′
∴∠AOD=∠ +∠ = ° ′
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
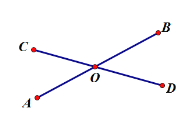
【题目】如图所示,直线AB、CD相交于点O,
(1)若∠AOC+∠BOD=90°,求∠BOC的度数
(2)若∠BOC比∠AOC的2倍多33°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D,过点D作DE∥AB交CA延长线于点E,连接AD,BD.

(1)△ABD的面积是________:
(2)求证:DE是⊙O的切线:
(3)求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,弦BC=2cm,∠ABC=60.
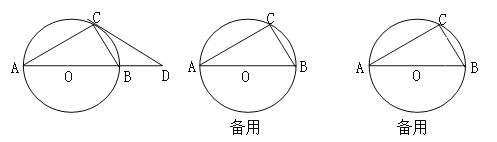
(1)求⊙O的直径;
(2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2cm/s的速度从点A出发沿着AB方向运动,同时动点F以1cm/s的速度从点B出发沿BC方向运动,设运动时间为t(s)(0<t<2),连结EF,当t为何值时,△BEF为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某制笔企业欲将200件产品运往![]() ,
,![]() ,
,![]() 三地销售,要求运往
三地销售,要求运往![]() 地的件数是运往
地的件数是运往![]() 地件数的2倍,各地的运费如图所示.设安排
地件数的2倍,各地的运费如图所示.设安排![]() 件产品运往
件产品运往![]() 地.
地.
|
|
| |
产品件数(件) |
|
| |
运费(元) |
|
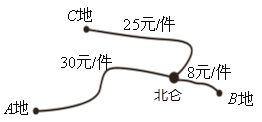
(1)①根据信息补全上表空格.②若设总运费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式及自变量的取值范围.
的函数关系式及自变量的取值范围.
(2)若运往![]() 地的产品数量不超过运往
地的产品数量不超过运往![]() 地的数量,应怎样安排
地的数量,应怎样安排![]() ,
,![]() ,
,![]() 三地的运送数量才能达到运费最少.
三地的运送数量才能达到运费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
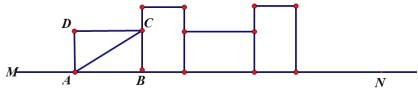
【题目】如图,在矩形ABCD中有对角线AC与BD相等,已知AB=4,BC=3,则有AB2+BC2=AC2,矩形在直线MN上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转至图②位置……依次类推,则:
(1)AC=__________.
(2)这样连续旋转2019次后,顶点B在整个旋转过程中所经过的路程之和是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上点A表示的数为6,B是数轴上在左侧的一点,且A,B两点间的距离为10。动点P从点A出发,以每秒6个单位长度的度沿数轴向左匀速运动,设运动时间为t![]() 秒。
秒。
![]()
(1)数轴上点B表示的数是______;当点P运动到AB的中点时,它所表示的数是_____。
(2)动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,求:
①当点P运动多少秒时,点P追上点Q?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
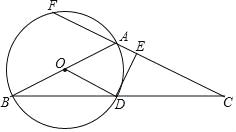
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE⊥AC;
(2)若DE+EA=8,⊙O的半径为10,求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:
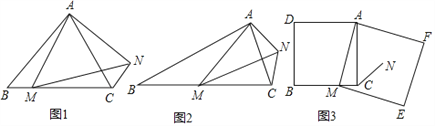
如图1,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为__________;
(2)深入探究:
如图2,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
(3)拓展延伸:
如图3,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN=![]() ,试求EF的长.
,试求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com