
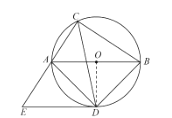
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D,过点D作DE∥AB交CA延长线于点E,连接AD,BD.

(1)△ABD的面积是________:
(2)求证:DE是⊙O的切线:
(3)求线段DE的长.
【答案】25 (2)见解析 (3)![]()
【解析】整体分析:
(1)判断△ABD是等腰直角三角形后,再求它的面积;(2)连接OD,证明∠ODE=90°;(3)过点A作AF⊥DE于点F,用tan∠EAF=tan∠CBA求EF即可.
解:(1)∵AB是直径,∴∠ACB=90°,
∵CD平分∠ACB,∴AD=BD,
∴S△ABD=![]() ×10×5=25;
×10×5=25;
(2)如图,连接OD,
∵AB为直径,CD平分∠ACB,∴∠ACD=45°,∴∠AOD=90°,
∵DE∥AB,∴∠ODE=90°,
∴OD⊥DE,∴DE是⊙O的切线;
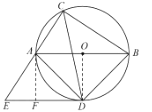
(3)∵AB=10,AC=6,∴BC=![]() =8,
=8,
过点A作AF⊥DE于点F,则四边形AODF是正方形,
∴AF=OD=FD=5,
∴∠EAF=90°﹣∠CAB=∠ABC,
∴tan∠EAF=tan∠CBA,
∴![]() ,即
,即![]() ,∴EF=15,
,∴EF=15,
∴DE=DF+EF=![]() +5=
+5=![]()


科目:初中数学 来源: 题型:
【题目】如今,网上购物已成为一种消费常态,纪念日饰品店想购买一种贺年卡在元旦时销售,在互联网上搜索了甲、乙两家网店(如图所示),已知两家网店的贺年卡质量相同,请看图回答下列问题:
甲 网 店 | 鼎发贺年卡 ¥1.00 产地:杭州 如实描述 信守天下 运费:8.00 七天退换 超过30个全部按六折 信用卡 最近售出11619个 |
乙 网 店 | 鼎发贺年卡 ¥0.80 产地:杭州 如实描述 信守天下 运费:8.00 七天退换 超过30个免运费 信用卡 最近售出10137个 |
(1)假如纪念日饰品店想购买x个贺年卡,那么在甲、乙两家网店分别需要花多少钱(用含x的式子表示)?(提示:如需付运费时,运费只需付一次,即8元)
(2)纪念日饰品店打算购买300个贺年卡,它应选择哪家网店省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
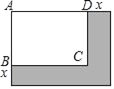
【题目】如图,矩形ABCD的长BC=5,宽AB=3.
(1)若矩形的长与宽同时增加2,则矩形的面积增加 .
(2)若矩形的长与宽同时增加x,此时矩形增加的面积为48,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
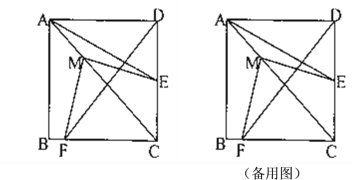
【题目】在正方形![]() 中,点
中,点![]() 是边
是边![]() 的中点,点
的中点,点![]() 是对角线
是对角线![]() 上的动点,连接
上的动点,连接![]() ,过点
,过点![]() 作
作![]() 交正方形的边于点
交正方形的边于点![]() ;
;
(1)当点![]() 在边
在边![]() 上时,①判断
上时,①判断![]() 与
与![]() 的数量关系;
的数量关系;
②当![]() 时,判断点
时,判断点![]() 的位置;
的位置;
(2)若正方形的边长为2,请直接写出点![]() 在
在![]() 边上时,
边上时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
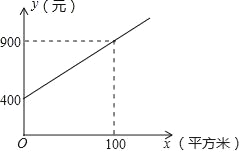
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
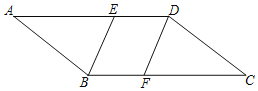
【题目】如图,ABCD中,DF平分∠ADC,交BC于点F,BE平分∠ABC,交AD于点E.
(1)求证:四边形BFDE是平行四边形;
(2)若∠AEB=68°,求∠C.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O是直线AB上一点,∠AOC=45°36’,OD平分∠BOC,求∠AOD的度数.完成下列推理过程:
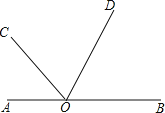
解:由题意可知,∠AOB是平角,
∠AOB= +∠BOC
因为∠AOC=45°36′
所以∠BOC= ° ′
又因为OD平分∠BOC
∴∠COD=![]() ∠BOC= ° ′
∠BOC= ° ′
∴∠AOD=∠ +∠ = ° ′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地。两车同时出发,匀速行驶。图2是客车、货车离C站的路程y![]() ,y
,y![]() (千米)与行驶时间x(小时)之间的函数关系图象。
(千米)与行驶时间x(小时)之间的函数关系图象。
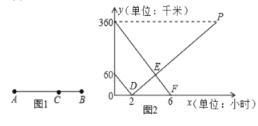
(1)填空:A,B两地相距___千米;货车的速度是___千米/时。
(2)求两小时后,货车离C站的路程y![]() 与行驶时间x之间的函数表达式;
与行驶时间x之间的函数表达式;
(3)客、货两车何时距离不大于30km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com