
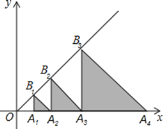
【题目】如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA2=1,则OA2015的长为____.
【答案】![]()
【解析】
根据△A1B1A2为等腰直角三角形,所以A1B1![]() OA2,A1B1=A1A2,然后根据等腰直角三角形斜边上的高等于斜边的一半求出A1B1、A1A2,同理求出A2B2,然后根据变化规律写出即可.
OA2,A1B1=A1A2,然后根据等腰直角三角形斜边上的高等于斜边的一半求出A1B1、A1A2,同理求出A2B2,然后根据变化规律写出即可.
因为△A1B1A2为等腰直角三角形,所以A1B1![]() OA2,A1B1=A1A2,又因为点B1在直线y=x上,所以OA1= A1B1,故OA1= A1A2,即点
OA2,A1B1=A1A2,又因为点B1在直线y=x上,所以OA1= A1B1,故OA1= A1A2,即点![]() 为OA2的中点,又因为OA2=1,所以A1B1=A1A2=
为OA2的中点,又因为OA2=1,所以A1B1=A1A2=![]() 。因为△A2B2A3为等腰直角三角形,所以A2B2
。因为△A2B2A3为等腰直角三角形,所以A2B2![]() OA2,,所以A1B1∥A1B2,所以A1B1为
OA2,,所以A1B1∥A1B2,所以A1B1为![]() △OA2B2的边A2B2上的中位线,所以A1B1=A1B2,即A2B2=2 A1B1,同理可证A3B3=2A2B2,同理可证AnBn=2An-1Bn-1,所以AnBn=2An-1Bn-1=2(2An-2Bn-2)==2n-2。当n=2014时,
△OA2B2的边A2B2上的中位线,所以A1B1=A1B2,即A2B2=2 A1B1,同理可证A3B3=2A2B2,同理可证AnBn=2An-1Bn-1,所以AnBn=2An-1Bn-1=2(2An-2Bn-2)==2n-2。当n=2014时,
A2014B2014=22014-2,因为△A2014B2014A2015为等腰直角三角形,所以A2014A2015=A2014B2014=22014-2且A2014B2014![]() OA2015因为点B2014在直线y=x上,所以OA2014= A2014B2014所以,OA2015=2A2014A2015=222012=22013故本题正确答案为22013。
OA2015因为点B2014在直线y=x上,所以OA2014= A2014B2014所以,OA2015=2A2014A2015=222012=22013故本题正确答案为22013。


科目:初中数学 来源: 题型:
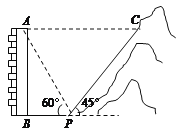
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30 m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
(1)求居民楼AB的高度;
(2)求C、A之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家将一种电视机按进价提高35%后定价,然后打出“九折酬宾,外送50元出租车费”的广告,结果每台电视机获利208元.
(1)求每台电视机的进价;
(2)另有一家商家出售同类产品,按进价提高40%,然后打出“八折酬宾”的广告,如果你想买这种产品,应选择哪一个商家?
查看答案和解析>>
科目:初中数学 来源: 题型:
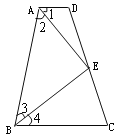
【题目】如图,四边形ABCD中,点E在边CD上,连结AE、BE.给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.
⑴用序号写出一个真命题(书写形式如:如果×××,那么××);并给出证明;
⑵用序号再写出三个真命题(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
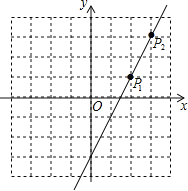
【题目】如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.
(1)写出点P2的坐标;
(2)求直线l所表示的一次函数的表达式;
(3)若将点P2先向右平移3个单位,再向上平移6个单位得到像点P3.请判断点P3是否在直线l上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市城市居民用电收费方式有以下两种:
(甲)普通电价:全天0.53元/度;
(乙)峰谷电价:峰时(早8:00~晚21:00)0.56元/度;谷时(晚21:00~早8:00)0.36元/度.
估计小明家下月总用电量为200度,
⑴若其中峰时电量为50度,则小明家按照哪种方式付电费比较合适?能省多少元?
⑵请你帮小明计算,峰时电量为多少度时,两种方式所付的电费相等?
⑶到下月付费时, 小明发现那月总用电量为200度,用峰谷电价付费方式比普通电价付费方式省了14元,求那月的峰时电量为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,直线![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,若
两点,若![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的角平分线,试说明:ME∥NF.
的角平分线,试说明:ME∥NF.
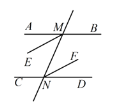
解:∵AB∥CD,(已知)
∴![]() ,( )
,( )
∵![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的角平分线,(已知)
的角平分线,(已知)
∴∠EMN= ∠AMN,
∠FNM= ∠DNM,(角平分线的定义)
∴![]() ,(等量代换)
,(等量代换)
∴ME∥NF,( )
由此我们可以得出一个结论:两条平行线被第三条直线所截,一对 角的平分线互相 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com