
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() .
.
求证:![]()
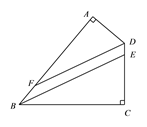
【答案】证明见解析.
【解析】
试题分析: 由四边形的内角和为360度求出∠ADC+∠ABC度数,由DF、BE分别为角平分线,利用角平分线定义及等量代换得到∠ABE+∠FDC为90度,再由直角三角形ADF两锐角互余及∠ADF=∠FDC,利用等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证.
试题解析:
在四边形ABCD中
∠A+∠ABC+∠C+∠ADC=360°
又∵ ∠A=∠ C=90°
∴∠ABC+∠ ADC=180°
在Rt△AFD中,∠AFD+∠ADF=90°
又∵DF平分∠ADC
∴∠ADF=![]() ∠ADC
∠ADC
所以∠AFD=90°-![]() ∠ADC=
∠ADC=![]() ∠ABC
∠ABC
又∵BE平分∠ABC
∴∠ABE=![]() ∠ABC
∠ABC
∴∠AFD=∠ABE
∴BE//DF


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】某学校积极响应正在开展的“创文活动”,组织甲、乙两个志愿工程队对所在社区的一些区域进行绿化改造,已知乙工程队每小时能完成的绿化面积是甲工程队每小时能完成的绿化面积的1.5倍,并且乙工程队完成200平方米的绿化面积比甲工程队完成200平方米的绿化面积少用2小时,甲工程队每小时能完成多少平方米的绿化面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
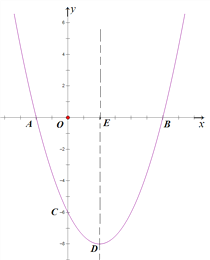
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ=![]() MN时,求菱形对角线MN的长.
MN时,求菱形对角线MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
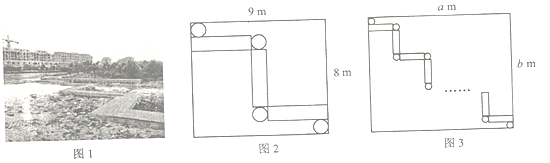
【题目】荷园新绿,曲径通幽,美丽的池塘逐渐成为城市生活小区中一抹靓丽的景观,幸福村在新农村建设中也计划建造一个长9![]() ,宽8
,宽8![]() 的长方形小荷池,并在池中修建如图2所示的步行曲桥,且步行曲桥中小圆的直径与小长方形的宽相等.
的长方形小荷池,并在池中修建如图2所示的步行曲桥,且步行曲桥中小圆的直径与小长方形的宽相等.
(1)求步行曲桥中小长方形的长与宽;
(2)经过村民代表讨论,决定扩大长方形荷池的面积,但保持步行曲桥中小圆与小长方形的形状与大小不变,只适当增加曲桥中小圆与小长方形的个数(如图3),若扩大后长方形荷池的长为![]()
![]() ,宽为
,宽为![]()
![]() ,直接写出
,直接写出![]() 与
与![]() 的数量关系:
的数量关系:
(3)若扩大后的长方形荷池,步行曲桥中共有![]() 个小长方形(
个小长方形(![]() 为正整数),求关于长方形荷池的周长
为正整数),求关于长方形荷池的周长![]() 与
与![]() 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师和小明同学玩数学游戏.老师取出一个不透明的口袋,口袋中装有三张分别标有数字1,2,3的卡片,卡片除数字外其余都相同,老师要求小明同学两次随机抽取一张卡片,并计算两次抽到卡片上的数字之积是奇数的概率.于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果.如图是小明同学所画的正确树状图的一部分.
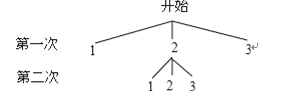
(1)补全小明同学所画的树状图;
(2)求小明同学两次抽到卡片上的数字之积是奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A, 0, B在同一条直线上,OD平分∠AOC, OE平分∠BOC.
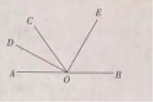
(1)若∠B0D=160°,求∠BOE的度数;
(2) 若∠COE比∠COD多60°.求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA2=1,则OA2015的长为____.
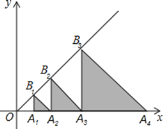
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+
x+![]() 与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,当⊙P与该直线相切时,点P坐标为___.
与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,当⊙P与该直线相切时,点P坐标为___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com