
【题目】如图,直线y=![]() x+
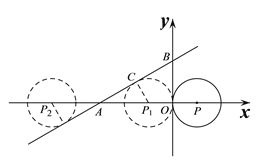
x+![]() 与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,当⊙P与该直线相切时,点P坐标为___.
与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,当⊙P与该直线相切时,点P坐标为___.

【答案】(-1,0),(-5,0);
【解析】分析:画出⊙P与直线AB相切时的图形,计算出AB与x轴的夹角,结合勾股定理和含30°角的直角的性质求AP1,AP2的长.
详解:如图,当圆心P运动到点P1,P2时,与直线AB相切.
当y=0时,![]() x+
x+![]() =0,解得x=-3,所以A(-3,0);
=0,解得x=-3,所以A(-3,0);
当x=0时,y=![]() ,所以B(0,
,所以B(0,![]() ).
).
Rt△ABO中,则勾股定理得AB=6,所以∠BAO=30°.
因为AB与⊙P1相切,所以∠ACP1=90°,所以AP1=2P1C=2.
所以OP1=3-2=1,则P1(-1,0).
同理AP2=2,则OP2=3+2=5,则P2(-5,0).
故答案为(-1,0),(-5,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我市城市居民用电收费方式有以下两种:
(甲)普通电价:全天0.53元/度;
(乙)峰谷电价:峰时(早8:00~晚21:00)0.56元/度;谷时(晚21:00~早8:00)0.36元/度.
估计小明家下月总用电量为200度,
⑴若其中峰时电量为50度,则小明家按照哪种方式付电费比较合适?能省多少元?
⑵请你帮小明计算,峰时电量为多少度时,两种方式所付的电费相等?
⑶到下月付费时, 小明发现那月总用电量为200度,用峰谷电价付费方式比普通电价付费方式省了14元,求那月的峰时电量为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】进入初中的学习,除了代数中学习了新的概念有理数,也开始了几何初步的学习,并且老师强调几何内容必须带齐作图工具,初一年级的学生沟通后觉得到网上买作图工具更方便更优惠些,一套如图的作图工具是2.3元/套,如果一次买100套以上(不含100套),售价是2.2元/套.
(1)列式表示买n套这样的作图工具所需钱数(注意对n的大小要有所考虑)
(2)按照这样的售价规定,会不会出现多买比少买反而付钱少的情况?
(3)如果需要买100套,怎样买更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
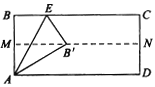
【题目】如图所示,将矩形ABCD纸对折,设折痕为MN,再把B点叠在折痕线MN上,(如图点B’),若![]() ,则折痕AE的长为( )
,则折痕AE的长为( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
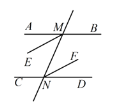
【题目】如图,已知直线AB∥CD,直线![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,若
两点,若![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的角平分线,试说明:ME∥NF.
的角平分线,试说明:ME∥NF.
解:∵AB∥CD,(已知)
∴![]() ,( )
,( )
∵![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的角平分线,(已知)
的角平分线,(已知)
∴∠EMN= ∠AMN,
∠FNM= ∠DNM,(角平分线的定义)
∴![]() ,(等量代换)
,(等量代换)
∴ME∥NF,( )
由此我们可以得出一个结论:两条平行线被第三条直线所截,一对 角的平分线互相 .
查看答案和解析>>
科目:初中数学 来源: 题型:
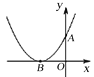
【题目】如图,已知二次函数![]() 的图象与y轴的正半轴交于点A,其顶点B在
的图象与y轴的正半轴交于点A,其顶点B在![]() 轴的负半轴上,且OA=OB,对于下列结论:①
轴的负半轴上,且OA=OB,对于下列结论:①![]() ≥0;②
≥0;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 无实数根;④
无实数根;④![]() 的最小值为3.其中正确结论的个数为( )
的最小值为3.其中正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com