练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

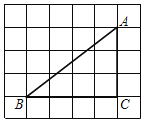
    【题目】如图，在6×5的网格（小正方形边长为1）中，Rt△ABC的三个顶点都在格点上．

    （1）在网格中，找到格点D，使四边形ACBD的面积为10，并画出这个四边形．

    （2）借助网格、只用直尺（无刻度）在AB上找一点E，使△AEC为等腰三角形，且AE＝AC．

    【答案】（1）见解析；（2）见解析

    【解析】

    （1）根据网格，即可找到格点D，使四边形ACBD的面积为10，并画出这个四边形；

    （2）借助网格、只用直尺即可在AB上找一点E，使△AEC为等腰三角形，且AE＝AC．

    （1）在点B上方两格处找到格点D，连接DA，如图，

    此时S四边形ADBC=S△ABD+S△ABC=

    四边形ACBD即为所求；

    （2）连接DC与AB交于点E，点E即为所求．如图，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为5，点A的坐标为（﹣4，0），点B在y轴上，若反比例函数y=（k≠0）的图象过点C，则该反比例函数的表达式为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

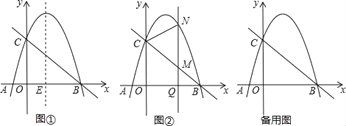
    【题目】如图①已知抛物线y=ax2﹣3ax﹣4a（a＜0）的图象与x轴交于A、B两点（A在B的左侧），与y的正半轴交于点C，连结BC，二次函数的对称轴与x轴的交点为E．

    （1）抛物线的对称轴与x轴的交点E坐标为_____，点A的坐标为_____；

    （2）若以E为圆心的圆与y轴和直线BC都相切，试求出抛物线的解析式；

    （3）在（2）的条件下，如图②Q（m，0）是x的正半轴上一点，过点Q作y轴的平行线，与直线BC交于点M，与抛物线交于点N，连结CN，将△CMN沿CN翻折，M的对应点为M′．在图②中探究：是否存在点Q，使得M′恰好落在y轴上？若存在，请求出Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

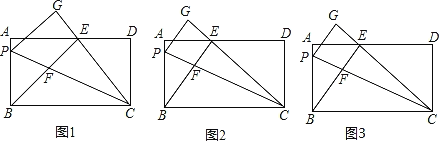
    【题目】在矩形ABCD中，AB＝12，P是边AB上一点，把△PBC沿直线PC折叠，顶点B的对应点是点G，过点B作BE⊥CG，垂足为E且在AD上，BE交PC于点F．

    （1）如图1，若点E是AD的中点，求证：△AEB≌△DEC；

    （2）如图2，当AD＝25，且AE＜DE时，求的值；

    （3）如图3，当BEEF＝108时，求BP的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

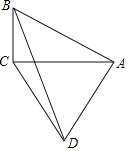
    【题目】如图，AC，BD为四边形ABCD的对角线，AC⊥BC，AB⊥AD，CA＝CD．若tan∠BAC＝．则tan∠DBC的值是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若三角形的一条角平分线与被平分的角的一边相等，则称这个三角形为“弱等腰三角形”，这条角平分线叫做这个三角形的“弱线”，如图①，AD是△ABC的角平分线，当AD＝AB时，则△ABC是“弱等腰三角形”，线段AD是△ABC的“弱线”．

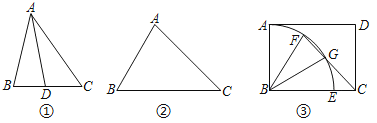
    （1）如图②，在△ABC中．∠B＝60°，∠C＝45°．求证：△ABC是“弱等腰三角形”；

    （2）如图③，在矩形ABCD中，AB＝3，BC＝4．以B为圆心在矩形内部作，交BC于点E，点F是上一点，连结CF．且CF与有另一个交点G．连结BG．当BG是△BCF的“弱线”时，求CG的长．

    （3）已知△ABC是“弱等腰三角形”，AD是“弱线”，且AB＝3BD，求AC：BC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某厂按用户需求生产一种产品，成本每件20万元，规定每件售价不低于成本，且不高于40万元。经市场调查，每年的销售量y（件）与每件售价x（万元）满足一次函数关系，部分数据如下表：

    售价x（万元/件）

    25

    30

    35

    销售量y（件）

    50

    40

    30

    （1）求y与x之间的函数表达式；

    （2）设商品每年的总利润为W（万元），求W与x之间的函数表达式（利润=收入-成本）；

    （3）试说明（2）中总利润W随售价x的变化而变化的情况，并指出售价为多少万元时获得最大利润，最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有4张相同的卡片，上面分别写有数字1、2、3、5，将卡片洗匀后背面朝上．

    (1)从中任意抽取1张，抽得的卡片上数字为奇数的概率是_______；

    (2)从中任意抽取1张，把上面的数字作为十位数，记录后不放回，再任意抽取1张把上面的数字作为个位数，求组成的两位数是3的倍数的概率．(用树状图或列表的方法)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明尝试用自己所学的知识检测车速，如图，他将观测点设在到公路l的距离为0.1千米的P处．一辆轿车匀速直线行驶过程中，小明测得此车从A处行驶到B处所用的时间为4秒，并测得∠APO＝59°，∠BPO＝45°．根据以上的测量数据，请求出该轿车在这4秒内的行驶速度．（参考数据：sin59°≈0.86，cos59°≈0.52，tan59°≈1.66）

    查看答案和解析>>

    同步练习册答案