
【题目】小明尝试用自己所学的知识检测车速,如图,他将观测点设在到公路l的距离为0.1千米的P处.一辆轿车匀速直线行驶过程中,小明测得此车从A处行驶到B处所用的时间为4秒,并测得∠APO=59°,∠BPO=45°.根据以上的测量数据,请求出该轿车在这4秒内的行驶速度.(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
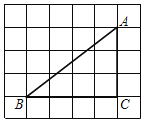
【题目】如图,在6×5的网格(小正方形边长为1)中,Rt△ABC的三个顶点都在格点上.
(1)在网格中,找到格点D,使四边形ACBD的面积为10,并画出这个四边形.
(2)借助网格、只用直尺(无刻度)在AB上找一点E,使△AEC为等腰三角形,且AE=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 是一个晾衣架的实物图,支架的基本图形是菱形,MN是晾衣架的一个滑槽,点P在滑槽MN上、下移动时,晾衣架可以伸缩,其示意图如图
是一个晾衣架的实物图,支架的基本图形是菱形,MN是晾衣架的一个滑槽,点P在滑槽MN上、下移动时,晾衣架可以伸缩,其示意图如图![]() 所示,已知每个菱形的边长均为20cm,且
所示,已知每个菱形的边长均为20cm,且![]() .
.

![]() 当点P向下滑至点N处时,测得
当点P向下滑至点N处时,测得![]() 时
时
![]() 求滑槽MN的长度;
求滑槽MN的长度;
![]() 此时点A到直线DP的距离是多少?
此时点A到直线DP的距离是多少?
![]() 当点P向上滑至点M处时,点A在相对于
当点P向上滑至点M处时,点A在相对于![]() 的情况下向左移动的距离是多少?
的情况下向左移动的距离是多少?
![]() 结果精确到
结果精确到![]() ,参考数据
,参考数据![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F分别在边CD、AB上,且满足CE=AF.
(1)求证:△ADE≌△CBF;
(2)连接AC,若AC恰好平分∠EAF,试判断四边形AECF为何种特殊的四边形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作体验)
如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°,如图②,小明的作图方法如下: 
第一步:分别以点A,B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA,OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于![]() ;
;
所以图中![]() 即为所求的点.(1)在图②中,连接
即为所求的点.(1)在图②中,连接![]() ,说明∠
,说明∠![]() =30°
=30°
(方法迁移)
(2)如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°,(不写做法,保留作图痕迹).
(深入探究)
(3)已知矩形ABCD,BC=2.AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为________.
(4)已知矩形ABCD,AB=3,BC=2,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数![]() (a是常数),有下列说法:
(a是常数),有下列说法:
①函数图象与坐标轴总有三个不同的交点;
②当x<1时,不是y随x的增大而增大就是y随x的增大而减小;
③若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数.
其中错误的说法是( )
A.①B.①②C.②③D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受新冠疫情影响,3月1日起,“君乐买菜”网络公司某种蔬菜的销售价格开始上涨.如图1,前四周该蔬菜每周的平均销售价格y(元/kg)与周次x(x是正整数,1≤x<5)的关系可近似用函数![]() 刻画;进入第5周后,由于外地蔬菜的上市,该蔬菜每周的平均销售价格y(元/kg)从第5周的6元/kg下降至第6周的5.6元/kg,y与周次x(5≤x≤7)的关系可近似用函数
刻画;进入第5周后,由于外地蔬菜的上市,该蔬菜每周的平均销售价格y(元/kg)从第5周的6元/kg下降至第6周的5.6元/kg,y与周次x(5≤x≤7)的关系可近似用函数![]() 刻画.
刻画.
(1)求a,b的值.
(2)若前五周该蔬菜的销售量m(kg)与每周的平均销售价格y(元/kg)之间的关系可近似地用如图2所示的函数图象刻画,第6周的销售量与第5周相同:
①求m与y的函数表达式;
②在前六周中,哪一周的销售额w(元)最大?最大销售额是多少?

(3)若该蔬菜第7周的销售量是100kg,由于受降雨的影响,此种蔬菜第8周的可销售量将比第7周减少a%(a>0).为此,公司又紧急从外地调运了5吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜第8周的销售价格比第7周仅上涨0.8a%.若在这一举措下,此种蔬菜在第8周的总销售额与第7周刚好持平,请通过计算估算出a的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2交x轴于点A(-1,0),B(n,0)(点A在点B的左边),交y轴于点C.
(1)当n=2时求△ABC的面积.
(2)若抛物线的对称轴为直线x=m,当1<n<4时,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com