
����Ŀ�����¹�����Ӱ�죬3��1������������������繫˾ij���߲˵����ۼ۸�ʼ���ǣ���ͼ1��ǰ���ܸ��߲�ÿ�ܵ�ƽ�����ۼ۸�y��Ԫ/kg�����ܴ�x��x����������1��x��5���Ĺ�ϵ�ɽ����ú���![]() �̻��������5�ܺ���������߲˵����У����߲�ÿ�ܵ�ƽ�����ۼ۸�y��Ԫ/kg���ӵ�5�ܵ�6Ԫ/kg�½�����6�ܵ�5.6Ԫ/kg��y���ܴ�x��5��x��7���Ĺ�ϵ�ɽ����ú���
�̻��������5�ܺ���������߲˵����У����߲�ÿ�ܵ�ƽ�����ۼ۸�y��Ԫ/kg���ӵ�5�ܵ�6Ԫ/kg�½�����6�ܵ�5.6Ԫ/kg��y���ܴ�x��5��x��7���Ĺ�ϵ�ɽ����ú���![]() �̻���
�̻���
��1����a��b��ֵ��
��2����ǰ���ܸ��߲˵�������m��kg����ÿ�ܵ�ƽ�����ۼ۸�y��Ԫ/kg��֮��Ĺ�ϵ�ɽ��Ƶ�����ͼ2��ʾ�ĺ���ͼ��̻�����6�ܵ����������5����ͬ��
����m��y�ĺ�������ʽ��
����ǰ�����У���һ�ܵ����۶�w��Ԫ�����������۶��Ƕ��٣�

��3�������߲˵�7�ܵ���������100kg�������ܽ����Ӱ�죬�����߲˵�8�ܵĿ����������ȵ�7�ܼ���a%��a��0����Ϊ�ˣ���˾�ֽ�������ص�����5�ִ����߲ˣ��պ����㱾���������Ҫ����ʹ�����߲˵�8�ܵ����ۼ۸�ȵ�7�ܽ�����0.8a%��������һ�ٴ��£������߲��ڵ�8�ܵ������۶����7�ܸպó�ƽ����ͨ����������a������ֵ��
���𰸡���1��4��![]() ����2����
����2����![]() �� �ڵ�2�ܻ��3�����۶����������۶���624Ԫ����3��15
�� �ڵ�2�ܻ��3�����۶����������۶���624Ԫ����3��15
��������
��1�����ô���ϵ����������⣻
��2�������ô���ϵ����������⣻
�ڷ�1��x��4��5��x��6����������ۣ��������۶�=������![]() ���ۼ۸������ö��κ�����������⼴�ɣ�
���ۼ۸������ö��κ�����������⼴�ɣ�
��3����������һԪ���η��̼����![]() ��ֵ�������ù��㷨������⣮
��ֵ�������ù��㷨������⣮
��1����(1��4.4)����![]() �ã�
�ã�![]() ��
��
��ã�![]() ��
��
��(5��6)����![]() �ã�
�ã�![]() ��
��
��ã�![]() ��
��
�ʴ�Ϊ��4��![]() ��
��
��2�����躯����ϵʽΪ��![]() ,
,
��(4.4��140)��(6��100)����ã�![]() ��
��
��ã�![]() ��
��
��m��y�ĺ�������ʽΪ��![]() ��
��
�ڵ�1��x��4ʱ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��x����������
�൱x=2��3ʱ��w�����ֵ624��
��x=5ʱ��![]() ��
��![]() ��
��
��5��x��6ʱ����![]() ��
��![]() ��
��
��![]() ��
��
��x����������5��x��6��
�൱x=5ʱ��w�����ֵ600��
�������ã���2�ܻ��3�����۶����������۶���624Ԫ��
��3��������ã�![]() ��
��
��ã�![]() ��
��![]() (��ȥ)��
(��ȥ)��
��![]() ��
��![]() ��6����29������25��
��6����29������25��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����û���������һ�ֲ�Ʒ���ɱ�ÿ��20��Ԫ���涨ÿ���ۼ۲����ڳɱ����Ҳ�����40��Ԫ�����г����飬ÿ���������y��������ÿ���ۼ�x����Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x����Ԫ/���� | 25 | 30 | 35 |
������y������ | 50 | 40 | 30 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW����Ԫ������W��x֮��ĺ�������ʽ������=����-�ɱ�����
��3����˵����2����������W���ۼ�x�ı仯���仯���������ָ���ۼ�Ϊ������Ԫʱ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ھ���OABC�У�OA=5��AB=4����DΪ��AB��һ�㣬����BCD��ֱ��CD�۵���ʹ��Bǡ������OA���ϵĵ�E�����ֱ���OC��OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ��
��1����OE�ij���
��2����O��D��C����������ߵĽ���ʽ��
��3��һ����P�ӵ�C��������CB��ÿ��2����λ�����ٶ����B�˶���ͬʱ����Q��E���������EC��ÿ��1����λ�����ٶ����C�˶�������P�����Bʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ��DP=DQ��
��4������N�ڣ�2���е������ߵĶԳ����ϣ���M���������ϣ��Ƿ���������ĵ�M���N��ʹ����M��N��C��EΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д��M������ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���������Լ���ѧ��֪ʶ���٣���ͼ�������۲�����ڵ���·l�ľ���Ϊ0.1ǧ��P����һ���γ�����ֱ����ʻ�����У�С����ô˳���A����ʻ��B�����õ�ʱ��Ϊ4�룬����á�APO��59������BPO��45�����������ϵIJ������ݣ�������ýγ�����4���ڵ���ʻ�ٶȣ����ο����ݣ�sin59���0.86��cos59���0.52��tan59���1.66��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ��k��0��ͼ����һ�κ���
��k��0��ͼ����һ�κ���![]() ͼ���ཻ��A��1��3����B��m��1�����㣮
ͼ���ཻ��A��1��3����B��m��1�����㣮
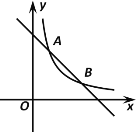
��1������������һ�κ����ı���ʽ��
��2����֪��P��a��0����a��0��������P��ƽ����y���ֱ�ߣ��ڵ�һ��������һ�κ���![]() ��ͼ���ཻ�ڵ�M���뷴��������
��ͼ���ཻ�ڵ�M���뷴��������![]() �ϵ�ͼ���ཻ�ڵ�N����PM��PN����Ϻ���ͼ��ֱ��д��a��ȡֵ��Χ��
�ϵ�ͼ���ཻ�ڵ�N����PM��PN����Ϻ���ͼ��ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽ������������ڼ䣬ijҩ������A��B�����ͺŵĿ��֣���֪����800ֻA�ͺ�450ֻB�͵�����Ϊ210Ԫ������400ֻA�ͺ�600ֻB�͵�����Ϊ180Ԫ��
��1����ÿֻA�Ϳ��ֺ�B�Ϳ��ֵ���������
��2����ҩ��ƻ�һ�ι��������ͺŵĿ��ֹ�2000ֻ������B�Ϳ��ֵĽ�����������A�Ϳ��ֵ�3�����蹺��A�Ϳ���xֻ����2000ֻ���ֵ�����������ΪyԪ��
����y����x�ĺ�����ϵʽ��
�ڸ�ҩ�깺��A�͡�B�Ϳ��ָ�����ֻ������ʹ�������������
��3��������ʱ����ҩ�꿪ʼʱ��B�Ϳ������100%�����ջسɱ���Ϊ�������������ߣ�������B�Ϳ��ֵ��ۼ۵���Ϊ���۵�15%����B�Ϳ��ֽ��۵ķ��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=x2+px+q�ĶԳ���Ϊֱ��x=��2�����䶥��M��һ��ֱ��y=kx+b��������ߵ���һ������ΪN����1����1������Ҫ��y������һ��P��ʹ��PM+PN��С�����P������Ϊ��������.
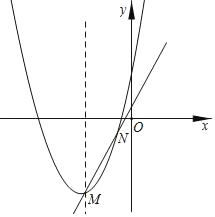
A. ��0����2�� B. ��0����![]() �� C. ��0����
�� C. ��0����![]() �� D. ��0����
�� D. ��0����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
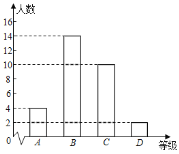
����Ŀ���ţ�1����40��ѧ������Ϊ4��ѧϰС�飬��ѧ�δ���������1��3��ѧ�������п�����ѧ�ɼ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ���£����µĵ�4С��10��ѧ���ɼ���δͳ�ƣ���10��ѧ���ɼ����£�60��65��72��75��75��75��86��86��96��99��
1��3��Ƶ���ֲ���
�ȼ� | ������ | Ƶ���������� |
D | 60��x��70 | 2 |
C | 70��x��80 | 10 |
B | 80��x��90 | 14 |
A | 90��x��100 | 4 |
����������Ϣ������������⣺
��1�����4С��10��ѧ���ɼ���������
��2�����������ѧ�δ�������ȫ��1��4��Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
1��4��Ƶ���ֲ���
�ȼ� | ������ | Ƶ���������� |
D | 60��x��70 | �� �� |
C | 70��x��80 | �� �� |
B | 80��x��90 | �� �� |
A | 90��x��100 | �� �� |
��3��ȫУ���꼶����600��ѧ���μ����п��ԣ����Ƹ�У��ѧ�ɼ�ΪA�ȼ���ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
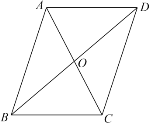
����Ŀ����һ����ѧ��У���ʦ��������ȫ��ͬ��ֽƬ��ֽƬ�Ϸֱ�д����ͼ��ʾͼ�ε�һ����������AD��BC����AB��DC����AO=OC��С��ͬѧ������ֽƬ�������ȡ���ţ���������״ͼ������ʾ����ȡ����ֽƬ�ϵ��������п��ܳ��ֵĽ��������ű�ʾ��������������������ı���ABCD��ƽ���ı��εĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com