
【题目】(操作体验)
如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°,如图②,小明的作图方法如下: 
第一步:分别以点A,B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA,OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于![]() ;
;
所以图中![]() 即为所求的点.(1)在图②中,连接
即为所求的点.(1)在图②中,连接![]() ,说明∠
,说明∠![]() =30°
=30°
(方法迁移)
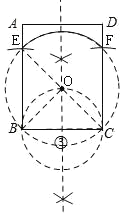
(2)如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°,(不写做法,保留作图痕迹).
(深入探究)
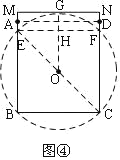
(3)已知矩形ABCD,BC=2.AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为________.
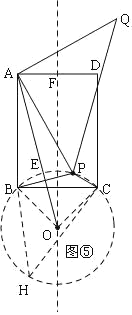
(4)已知矩形ABCD,AB=3,BC=2,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为________.
【答案】(1)见解析;(2)见解析;(3)2≤m<![]() ;(4)
;(4)![]() .
.
【解析】
(1)先根据等边三角形得:∠AOB=60°,则根据圆周角定理可得:∠![]() =30°;
=30°;
(2)先作等腰直角三角形BEC、BFC,再作△EBC的外接圆,可得圆心角∠BOC=90°,则![]() 所对的圆周角都是45°;
所对的圆周角都是45°;
(3)先确定⊙O,根据同弧所对的圆周角相等可得AD在四边形GEFH内部时符合条件;
(4)先确定⊙O,根据圆周角定理正确画出∠BPC=135°,利用勾股定理求OF的长,知道A、P、O在同一直线上时,AP最小,则PQ的值最小,求AE的长,即是AP的长,可得PQ的最小值.
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°,
由图②得:∠![]() =
=![]() ∠AOB=30°;
∠AOB=30°;
如图③,①以B、C为圆心,以BC为半径作圆,交AB、DC于E、F,
②作BC的中垂线,连接EC,交于O,
③以O为圆心,OE为半径作圆,
则![]() 上所有的点(不包括E、F两点)即为所求;
上所有的点(不包括E、F两点)即为所求;
如图④,同理作⊙O,
∵BE=BC=2,
∴CE=![]() ,
,
∴⊙O的半径为![]() ,即OE=OG=
,即OE=OG=![]() ,
,
∵OG⊥EF,
∴EH=1,
∴OH=1,
∴GH=![]() ,
,
∴BE≤AD<MN,
∴2≤m<![]() ,即2≤m<
,即2≤m<![]() ,
,
故答案为:2≤m<![]() ;
;
如图⑤,构建⊙O,使∠COB=90°,在优弧![]() 上取一点H,则∠CHB=45°
上取一点H,则∠CHB=45°
∴∠CPB=135°,
由旋转得:△APQ是等腰直角三角形,
∴PQ=![]() AP,
AP,
∴PQ取最小值时,就是AP取最小值,
当P与E重合时,即A、P、O在同一直线上时,AP最小,则PQ的值最小,
在Rt△AFO中,AF=1,OF=3+1=4,
∴AO=![]() ,
,
∴AE=![]() =AP,
=AP,
∴PQ=![]() AP=
AP=![]() =
=![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
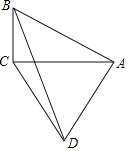
【题目】如图,AC,BD为四边形ABCD的对角线,AC⊥BC,AB⊥AD,CA=CD.若tan∠BAC=![]() .则tan∠DBC的值是( )
.则tan∠DBC的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张圆形纸片,小芳进行了如下连续操作:
![]() 将圆形纸片左右对折,折痕为AB,如图
将圆形纸片左右对折,折痕为AB,如图![]() .
.
![]() 将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图
将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图![]() .
.
![]() 将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图
将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图![]() .
.
![]() 连结AE、AF、BE、BF,如图
连结AE、AF、BE、BF,如图![]() .
.
经过以上操作,小芳得到了以下结论:
![]() ;
;![]() 四边形MEBF是菱形;
四边形MEBF是菱形;![]() 为等边三角形;
为等边三角形;![]() :
:![]() :
:![]() .以上结论正确的有
.以上结论正确的有![]()
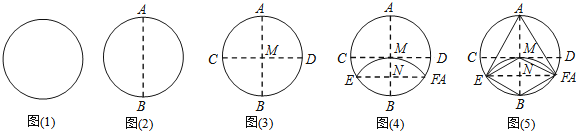
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长.
(2)求经过O,D,C三点的抛物线的解析式.
(3)一动点P从点C出发,沿CB以每秒2个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t秒,当t为何值时,DP=DQ.
(4)若点N在(2)中的抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E为顶点的四边形是平行四边形?若存在,直接写出M点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明尝试用自己所学的知识检测车速,如图,他将观测点设在到公路l的距离为0.1千米的P处.一辆轿车匀速直线行驶过程中,小明测得此车从A处行驶到B处所用的时间为4秒,并测得∠APO=59°,∠BPO=45°.根据以上的测量数据,请求出该轿车在这4秒内的行驶速度.(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (k≠0)图象与一次函数
(k≠0)图象与一次函数![]() 图象相交于A(1,3),B(m,1)两点.
图象相交于A(1,3),B(m,1)两点.
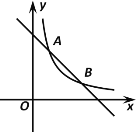
(1)求反比例函数和一次函数的表达式.
(2)已知点P(a,0)(a>0),过点P作平行于y轴的直线,在第一象限内与一次函数![]() 的图象相交于点M,与反比例函数
的图象相交于点M,与反比例函数![]() 上的图象相交于点N.若PM>PN,结合函数图象直接写出a的取值范围.
上的图象相交于点N.若PM>PN,结合函数图象直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+px+q的对称轴为直线x=﹣2,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(﹣1,﹣1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( ).
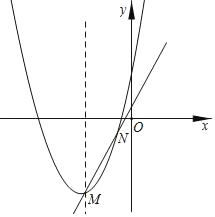
A. (0,﹣2) B. (0,﹣![]() ) C. (0,﹣
) C. (0,﹣![]() ) D. (0,﹣
) D. (0,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数图象的顶点坐标为C(1,﹣2),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,0),B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
(1)求这个二次函数的解析式;
(2)设点P的横坐标为x,求线段PE的长(用含x 的代数式表示);
(3)点D为直线AB与这个二次函数图象对称轴的交点,若以点P、E、D为顶点的三角形与△AOB相似,请求出P点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com