
����Ŀ����֪����ͼ�����κ���ͼ��Ķ�������ΪC��1����2����ֱ��y=kx+m��ͼ����ö��κ�����ͼ����A��B���㣬����A������Ϊ��3��0����B����y���ϣ���PΪ�߶�AB�ϵ�һ�����㣨��P���A��B���غϣ�������P�Ҵ�ֱ��x���ֱ����������κ�����ͼ���ڵ�E��
��1����������κ����Ľ���ʽ��
��2�����P�ĺ�����Ϊx�����߶�PE�ij����ú�x �Ĵ���ʽ��ʾ����
��3����DΪֱ��AB��������κ���ͼ��Գ���Ľ��㣬���Ե�P��E��DΪ��������������AOB���ƣ������P������꣮

���𰸡���1��y=![]() ��x��1��2��2����2��PE=��
��x��1��2��2����2��PE=��![]() x2+
x2+![]() x����3��P��������
x����3��P��������![]() ��1��
��1��![]() ����1+
����1+![]() ��
��![]() ��1����
��1����
��������
(1)���ô���ϵ��������κ�������ʽ.(2)�����ֱ��AB���̣������PE��.(3)�������Ƶ����ʣ��б���ʽ���ٴ��룬�ⷽ�̣������P������.
��1������κ����Ľ���ʽΪy=a��x��1��2��2��
��A��3��0�����������ϣ�
��0=a��3��1��2��2
��a=![]() ��
��
��y=![]() ��x��1��2��2��
��x��1��2��2��
��2����������y�ύ��B������Ϊ��0��![]() ����
����
��ֱ��AB�Ľ���ʽΪy=kx+m��
��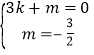 ,
,
��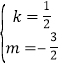 ,
,
��ֱ��AB�Ľ���ʽΪy=![]() .
.
��PΪ�߶�AB�ϵ�һ�����㣬
��P��������x��![]() x��
x��![]() .������0��x��3��
.������0��x��3��
�������֪PE��y�ᣬ��E������Ϊ��x��![]() x2��x��
x2��x��![]() ����
����
��0��x��3��
��PE=��![]() .������
.������![]() x2��x��
x2��x��![]() ��=��
��=��![]() x2+
x2+![]() .
.
��3���������֪D�������Ϊx=1����D����ֱ��AB�ϣ�
��D�����꣨1����1����
����EDP=90��ʱ����AOB�ס�EDP��
��![]() .
.
����D��DQ��PE��Q��
��xQ=xP=x��yQ=��1��
���DQP�ס�AOB�ס�EDP��
��![]() ,
,
��OA=3��OB=![]() ��AB=
��AB=![]() ,
,
��DQ=x��1��
��DP=![]() ��x��1����
��x��1����
��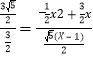 ,
,
��ã�x=��1��![]() ����ֵ��ȥ����
����ֵ��ȥ����
��P��![]() ��1��
��1��![]() ������ͼ�е�P1�㣩��
������ͼ�е�P1�㣩��
������DEP=90��ʱ����AOB�ס�DEP��
��![]() .
.
�ɣ�2��PE=��![]() x2+
x2+![]() .��DE=x��1��
.��DE=x��1��
��![]()
��ã�x=1��![]() ������ֵ��ȥ����
������ֵ��ȥ����
��P��1+![]() ��
��![]() ��1������ͼ�е�P2�㣩��
��1������ͼ�е�P2�㣩��
����������P��������![]() ��1��
��1��![]() ����1+
����1+![]() ��
��![]() ��1����
��1����


 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽���������ȡ���ŵ�����Ҫ;������ij�м��߿�չ��һ�γ������飬���ݵ����������������в�������ͳ��ͼ��

����������Ϣ����������⣺
��1����γ������������������������ͨ�����������˽����ŵ�����ռ�����������İٷֱ�Ϊ����������ͳ��ͼ�У����ֻ�����������Ӧ��Բ�ĽǵĴ�С�������ȣ�
��2���벹ȫ����ͳ��ͼ��
��3��������Լ��950���ˣ�������������ж������˽������Ժ��ֻ���������Ϊ����ȡ���ŵ�����Ҫ;������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʡ�����Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μ�ȫ����������
���ǽ��������β��ԣ����Գɼ����±�����λ��������
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 10 | 8 | 9 | 8 | 10 | 9 |
�� | 10 | 7 | 10 | 10 | 9 | 8 |
��1�����ݱ����е����ݣ��������ƽ���ɼ��� �����ҵ�ƽ���ɼ��� ����
��2���ֱ����ס������β��Գɼ��ķ��
��3�����ݣ�1������2������Ľ��������Ϊ�Ƽ�˭�μ�ȫ�����������ʣ���˵�����ɣ�
�����㷽��Ĺ�ʽ��s2��![]() ��
��![]() �ݣ�
�ݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У������²�����ͼ���ֱ���B��CΪԲ�ģ��Դ���![]() BC�ij�Ϊ�뾶������������������M��N���㣬��ֱ��MN�����AC��BC�ֱ���D��E���㣬����BD��AE������BAC=90����������˵���У�
BC�ij�Ϊ�뾶������������������M��N���㣬��ֱ��MN�����AC��BC�ֱ���D��E���㣬����BD��AE������BAC=90����������˵���У�
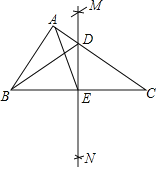
��EΪ��ABC���Բ��Բ�ģ�
��ͼ����4�����������Σ�
����ABE�ǵȱ������Σ�
�ܵ���C=30��ʱ��BD��ֱ��ƽ��AE��
������ȷ���У�������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���BCD��100������B��60o������AC��BC��AC��AB���ҡ�ABC�ա�ADC��CE��CF�ֱ��ǡ�ACB���ACD��ƽ���ߣ��ֱ�AB��AD��E��F����.
(1)�ֱ����BAD�͡�AEC�Ķ���.
(2)��д��ͼ��������ȵ��߶�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AC��BD�ཻ�ڵ�O����E��OA���е㣬����BE���ӳ���AD�ڵ�F����֪S��AEF=4�������н��ۣ���![]() ����S��BCE=36����S��ABE=12���ܡ�AEF����ACD������һ����ȷ���ǣ�������
����S��BCE=36����S��ABE=12���ܡ�AEF����ACD������һ����ȷ���ǣ�������

A. �٢ڢۢ� B. �٢� C. �ڢۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��BD��CD��BD

��1����AB=9��CD=4��BD=10��������BD���Ƿ����P�㣬ʹ��P��A��B����Ϊ���������������P��C��D����Ϊ��������������ƣ������ڣ���BP�ij����������ڣ���˵�����ɣ�
��2����AB=9��CD=4��BD=12��������BD�ϴ��ڶ��ٸ�P�㣬ʹ��P��A��B����Ϊ���������������P��C��D����Ϊ��������������ƣ�����BP�ij���
��3����AB=9��CD=4��BD=15��������BD�ϴ��ڶ��ٸ�P�㣬ʹ��P��A��B����Ϊ���������������P��C��D����Ϊ��������������ƣ�����BP�ij���
��4����AB=m��CD=n��BD=l������m��n��l����ʲô��ϵʱ��������P��A��B����Ϊ���������������P��C��D����Ϊ��������������Ƶ�һ��P�㣿����P�㣿����P�㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����Ϊ����3����6����������y=ax2+bx+c�����㣨��1����4���������н����д�����ǣ�������

A. b2��4ac
B. ax2+bx+c�ݩ�6
C. ���㣨��2��m��������5��n�����������ϣ���m��n
D. ����x��һԪ���η���ax2+bx+c=��4������Ϊ��5�ͩ�1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�½���վվǰ�㳡��Ҫ�̻������Ϊ46000��2��ʩ�������̻���22000��2��ÿ��Ĺ���������Ϊԭ����1.5���������ǰ4������˸����̻����̣�
��1�������̻�����ԭ�ƻ�ÿ����ɶ�����2��
��2�������̻���������һ�鳤Ϊ20�ף���Ϊ8�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ����ǵ����֮��Ϊ56��2�������̵�֮�估�ܱ����п�����ȵ�����ͨ������ͼ��ʾ����������ͨ���Ŀ����Ƕ����ף�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com