
����Ŀ��һ��Բ��ֽƬ��С����������������������
![]() ��Բ��ֽƬ���Ҷ��ۣ��ۺ�ΪAB����ͼ
��Բ��ֽƬ���Ҷ��ۣ��ۺ�ΪAB����ͼ![]() ��
��
![]() ��Բ��ֽƬ�����۵���ʹA��B�����غϣ��ۺ�CD��AB�ཻ��M����ͼ
��Բ��ֽƬ�����۵���ʹA��B�����غϣ��ۺ�CD��AB�ཻ��M����ͼ![]() ��
��
![]() ��Բ��ֽƬ��EF�۵���ʹB��M�����غϣ��ۺ�EF��AB�ཻ��N����ͼ
��Բ��ֽƬ��EF�۵���ʹB��M�����غϣ��ۺ�EF��AB�ཻ��N����ͼ![]() ��
��
![]() ����AE��AF��BE��BF����ͼ
����AE��AF��BE��BF����ͼ![]() ��
��
�������ϲ�����С���õ������½��ۣ�
![]() ��
��![]() �ı���MEBF�����Σ�
�ı���MEBF�����Σ�![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�![]() ��
��![]() ��
��![]() �����Ͻ�����ȷ����
�����Ͻ�����ȷ����![]()
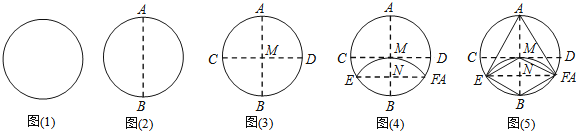
A.1��B.2��C.3��D.4��
���𰸡�D
��������
�����۵������ʿɵá�BMD=��BNF=90�㣬Ȼ������ͬλ����ȣ���ֱ��ƽ�пɵ�CD��EF���Ӷ��ж�����ȷ��
���ݴ��������ɵ�BM��ֱƽ��EF�������BN=MN���Ӷ��õ�BM��EF���ഹֱƽ�֣�Ȼ����ݶԽ����ഹֱƽ�ֵ��ı�������������ı���MEBF�����Σ��Ӷ��õ�����ȷ������ֱ��������![]() �����Ե�ֱ�DZߵ���б�ߵ�һ�������MEN=30�㣬Ȼ�������EMN=60�㣬���ݵȱ߶ԵȽ������AEM=��EAM��Ȼ�����������ε�һ����ǵ������������ڵ������ڽǵĺ������AEM=30�㣬�Ӷ��õ���AEF=60�㣬ͬ�������AFE=60�����ٸ��������ε��ڽǺ͵���180�������EAF=60�����Ӷ��ж���AEF�ǵȱ������Σ�����ȷ��
�����Ե�ֱ�DZߵ���б�ߵ�һ�������MEN=30�㣬Ȼ�������EMN=60�㣬���ݵȱ߶ԵȽ������AEM=��EAM��Ȼ�����������ε�һ����ǵ������������ڵ������ڽǵĺ������AEM=30�㣬�Ӷ��õ���AEF=60�㣬ͬ�������AFE=60�����ٸ��������ε��ڽǺ͵���180�������EAF=60�����Ӷ��ж���AEF�ǵȱ������Σ�����ȷ��
��Բ�İ뾶Ϊr�����EN= ![]() ����ɵ�EF=2EN=
����ɵ�EF=2EN=![]() �����ɵ�S�ı���AEBF��S����BEMF�Ĵ𰸣����Ԣ���ȷ��
�����ɵ�S�ı���AEBF��S����BEMF�Ĵ𰸣����Ԣ���ȷ��
�⣺��ֽƬ�����۵�A��B�����غϣ�
���BMD=90�㣬
��ֽƬ��EF�۵���B��M�����غϣ�
���BNF=90�㣬
���BMD=��BNF=90�㣬
��CD��EF���ʢ���ȷ��
���ݴ���������BM��ֱƽ��EF��
�֡�ֽƬ��EF�۵���B��M�����غϣ�
��BN=MN�� ��BM��EF���ഹֱƽ�֣�
���ı���MEBF�����Σ��ʢ���ȷ��
��ME=MB=2MN��
���MEN=30�㣬
���EMN=90��-30��=60�㣬
�֡�AM=ME�����ǰ뾶����
���AEM=��EAM��
���AEM=![]() ��EMN=
��EMN=![]() ��60��=30����
��60��=30����
���AEF=��AEM+��MEN=30��+30��=60����
ͬ�������AFE=60���� ���EAF=60����
���AEF�ǵȱ������Σ��ʢ���ȷ��
��Բ�İ뾶Ϊr����EN=![]() �� ��EF=2EN=
�� ��EF=2EN=![]() ��
��
��S�ı���AEBF��S����BEMF=![]()
�ʢ���ȷ��
����������������ȷ���Ǣ٢ڢܹۢ�4����
��ѡ��D��


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������D��AB���ӳ����ϣ�C��E�ǡ�O�ϵ����㣬CE=CB����BCD=��CAE���ӳ�AE��BC���ӳ����ڵ�F��
��1����֤��CD�ǡ�O�����ߣ�
��2����֤��CE=CF��
��3����BD=1��CD=![]() ������AC�ij���
������AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���BCA��90�㣬AC��BC����D��BC���е㣬��F���߶�AD�ϣ�DF��CD��BF��CA��E�㣬����A��DA�Ĵ��߽�CF���ӳ����ڵ�G�����н��ۣ���CF2��EFBF����AG��2DC����AE��EF����AFEC��EFEB��������ȷ�Ľ����У�������
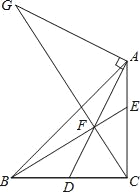
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ʾ����![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �Ľ�ƽ���ߣ���
�Ľ�ƽ���ߣ���![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ������
������![]() ��
��![]() ��
��
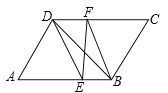
��1����֤��![]() ��
��![]() ����ƽ�֣�
����ƽ�֣�
��2����![]() ��
��![]() ��
��![]() �����߶�
�����߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
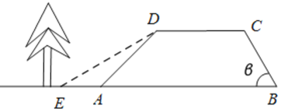
����Ŀ��ˮ�ӵĺ����������ABCD���ֲ�ðӶ�DC=4 m������AD���¶�iΪ1:1������BC���½���Ϊ60�����Ӹ�3m��(![]() )��
)��
(1)�ӵ�AB�ij�(��ȷ��0��1)��
(2)ˮ������Ϊ�˼ӹ�ˮ�ӣ��ڱ��ְӶ�CD���������½���AD���¶�(��ͼ)��ʹ������DE���¶�iΪ![]() ��ԭˮ�ӵײ���ǰ��2.5m����һǧ��������˼ӹ̹��̶Թ����Ƿ���Ӱ�죿��˵�����ɣ�
��ԭˮ�ӵײ���ǰ��2.5m����һǧ��������˼ӹ̹��̶Թ����Ƿ���Ӱ�죿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ��һ�����¼ܵ�ʵ��ͼ��֧�ܵĻ���ͼ�������Σ�MN�����¼ܵ�һ�����ۣ���P�ڻ���MN�ϡ����ƶ�ʱ�����¼ܿ�����������ʾ��ͼ��ͼ
��һ�����¼ܵ�ʵ��ͼ��֧�ܵĻ���ͼ�������Σ�MN�����¼ܵ�һ�����ۣ���P�ڻ���MN�ϡ����ƶ�ʱ�����¼ܿ�����������ʾ��ͼ��ͼ![]() ��ʾ����֪ÿ�����εı߳���Ϊ20cm����
��ʾ����֪ÿ�����εı߳���Ϊ20cm����![]() ��
��

![]() ����P���»�����N��ʱ�����
����P���»�����N��ʱ�����![]() ʱ
ʱ
![]() ��MN�ij��ȣ�
��MN�ij��ȣ�
![]() ��ʱ��A��ֱ��DP�ľ����Ƕ��٣�
��ʱ��A��ֱ��DP�ľ����Ƕ��٣�
![]() ����P���ϻ�����M��ʱ����A�������
����P���ϻ�����M��ʱ����A�������![]() ������������ƶ��ľ����Ƕ��٣�
������������ƶ��ľ����Ƕ��٣�
![]() �����ȷ��
�����ȷ��![]() ���ο�����
�������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2![]() x+m=0,����������ȵ�ʵ����.
x+m=0,����������ȵ�ʵ����.
����ʵ��m���������ֵ��
���ڢŵ����£����̵�ʵ������x1��x2,�����ʽx12+x22��x1x2��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������飩
��ͼ�٣���֪�߶�AB��ֱ��l����ֱ�ߺ�Բ����l���������еĵ�P��ʹ�á�APB=30������ͼ�ڣ�С������ͼ�������£� 
��һ�����ֱ��Ե�A��BΪԲ�ģ�AB��Ϊ�뾶������������AB�Ϸ����ڵ�O��
�ڶ���������OA��OB��
����������OΪԲ�ģ�OA��Ϊ�뾶����O����l��![]() ��
��
����ͼ��![]() ��Ϊ����ĵ㣮��1����ͼ���У�����
��Ϊ����ĵ㣮��1����ͼ���У�����![]() ��˵����
��˵����![]() =30��
=30��
������Ǩ�ƣ�
��2����ͼ�ۣ���ֱ�ߺ�Բ���ھ���ABCD���������еĵ�P��ʹ�á�BPC=45��������д������������ͼ�ۼ�����
������̽����
��3����֪����ABCD��BC=2��AB=m��PΪAD���ϵĵ㣬�������BPC=45���ĵ�Pǡ����������m��ȡֵ��ΧΪ________��
��4����֪����ABCD��AB=3��BC=2��PΪ����ABCD��һ�㣬�ҡ�BPC=135��������P�Ƶ�A��ʱ����ת90������Q����PQ����СֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��PΪ���κ���y��x2��2x��3ͼ����һ�㣬��������κ�����ͼ����x�ύ��A��B���㣨A��B���Ҳࣩ����y�ύ��C�㣬����APCΪֱ����������ACΪֱ�DZߣ����P�ĺ������ֵΪ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com