
【题目】已知点P为二次函数y=x2﹣2x﹣3图象上一点,设这个二次函数的图象与x轴交于A,B两点(A在B的右侧),与y轴交于C点,若△APC为直角三角形且AC为直角边,则点P的横坐标的值为_____.
【答案】﹣1或﹣2
【解析】
分∠ACP为直角、∠PAC为直角两种情况,利用直线与抛物线的交点求解即可.
解:对于y=x2﹣2x﹣3①,令y=0,则x=3或﹣1,令x=0,则y=﹣3,
故点A、B、C的坐标分别为:(3,0)、(﹣1,0)、(0,﹣3).
①当∠ACP为直角时,如下图,
由点A、C的坐标知,OA=OC=3,即直线AC的与x轴负半轴的夹角为45°,
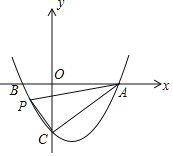
而∠ACP为直角,故直线PC的倾斜角为45°,
故设直线PC的表达式为:y=﹣x+b,将点C的坐标代入上式并解得:b=﹣3,
故直线PC的表达式为:y=﹣x﹣3②,
联立①②并解得:x=0或﹣1(舍去0),
故点P的坐标为:(﹣1,0);
②当∠PAC为直角时,
同理可得:点P(﹣2,5);
故答案为:﹣1或﹣2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一张圆形纸片,小芳进行了如下连续操作:
![]() 将圆形纸片左右对折,折痕为AB,如图
将圆形纸片左右对折,折痕为AB,如图![]() .
.
![]() 将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图
将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图![]() .
.
![]() 将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图
将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图![]() .
.
![]() 连结AE、AF、BE、BF,如图
连结AE、AF、BE、BF,如图![]() .
.
经过以上操作,小芳得到了以下结论:
![]() ;
;![]() 四边形MEBF是菱形;
四边形MEBF是菱形;![]() 为等边三角形;
为等边三角形;![]() :
:![]() :
:![]() .以上结论正确的有
.以上结论正确的有![]()
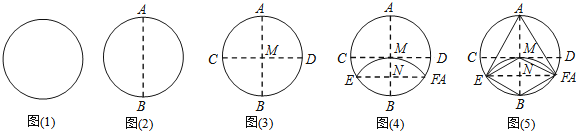
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (k≠0)图象与一次函数
(k≠0)图象与一次函数![]() 图象相交于A(1,3),B(m,1)两点.
图象相交于A(1,3),B(m,1)两点.
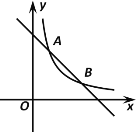
(1)求反比例函数和一次函数的表达式.
(2)已知点P(a,0)(a>0),过点P作平行于y轴的直线,在第一象限内与一次函数![]() 的图象相交于点M,与反比例函数
的图象相交于点M,与反比例函数![]() 上的图象相交于点N.若PM>PN,结合函数图象直接写出a的取值范围.
上的图象相交于点N.若PM>PN,结合函数图象直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+px+q的对称轴为直线x=﹣2,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(﹣1,﹣1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( ).
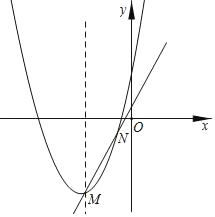
A. (0,﹣2) B. (0,﹣![]() ) C. (0,﹣
) C. (0,﹣![]() ) D. (0,﹣
) D. (0,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
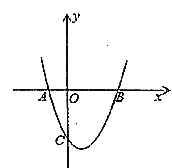
(1)求该抛物线的解析式;
(2)抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(3)设抛物线上有一个动点![]() ,当点
,当点![]() 在该抛物线上滑动到什么位置时,满足
在该抛物线上滑动到什么位置时,满足![]() ,并求出此时点
,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
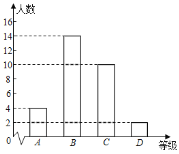
【题目】九(1)班40名学生共分为4个学习小组,数学课代表制作了1~3组学生的期中考试数学成绩频数分布表和频数分布直方图如下.余下的第4小组10名学生成绩尚未统计,这10名学生成绩如下:60,65,72,75,75,75,86,86,96,99.
1~3组频数分布表
等级 | 分数段 | 频数(人数) |
D | 60≤x<70 | 2 |
C | 70≤x<80 | 10 |
B | 80≤x<90 | 14 |
A | 90≤x<100 | 4 |
根据以上信息,解答下列问题:
(1)求第4小组10名学生成绩的众数;
(2)请你仿照数学课代表制作全班1~4组频数分布表和频数分布直方图;
1~4组频数分布表
等级 | 分数段 | 频数(人数) |
D | 60≤x<70 |
|
C | 70≤x<80 |
|
B | 80≤x<90 |
|
A | 90≤x<100 |
|
(3)全校九年级共有600名学生参加期中考试,估计该校数学成绩为A等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权利,我国海监部门对中国海域实现常态化管理.某日,我国海监船在某海岛附近的海域执行巡逻任务.如图,此时海监船位于海岛P的北偏东30°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的南偏东45°方向的B处,求海监船航行了多少海里(结果保留根号)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数图象的顶点坐标为C(1,﹣2),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,0),B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
(1)求这个二次函数的解析式;
(2)设点P的横坐标为x,求线段PE的长(用含x 的代数式表示);
(3)点D为直线AB与这个二次函数图象对称轴的交点,若以点P、E、D为顶点的三角形与△AOB相似,请求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分已知关于x的一元二次方程(m-2)x2+(2m+1)x+m=0有两个实数根x1,x2.
(1)求m的取值范围.
(2)若|x1|=|x2|,求m的值及方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com